المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Quiteprime |
 1144
 04:06 مساءً
date: 19-1-2021 |
Author : Sloane, N. J. A. 
Book or Source : Sequences A050260 and A050261 in "The On-Line Encyclopedia of Integer Sequences." 
Page and Part : ...|
Read More
Date: 26-4-2020
713
Date: 5-12-2020
784
Date: 27-1-2021
1131
|
A positive integer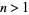 
is quiteprime iff all primes 
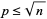satisfy
![|2[n (mod p)]-p|<=p+1-sqrt(p).](https://mathworld.wolfram.com/images/equations/Quiteprime/NumberedEquation1.gif) |
Also define 2 and 3 to be quiteprimes. Then the first few quiteprimes are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 137, ... (OEIS A050260), and the first few primes which are not quiteprimes are 131, 181, 197, 199, 233, 241, 263, 307, 311, 313, 331, 337, 353, 373, 379, ... (OEIS A050261).
REFERENCES:
Ferry, J. "RE: Veryprimes defined." sci.math posting, 09 Sep 1999.
Sloane, N. J. A. Sequences A050260 and A050261 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
مشاتل الكفيل تزيّن مجمّع أبي الفضل العبّاس (عليه السلام) بالورد استعدادًا لحفل التخرج المركزي
|
|
|
