المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Bolyai Expansion |
 539
 05:18 مساءً
date: 26-4-2020 |
Author : Martin, G. 
Book or Source : "The Unreasonable Effectualness of Continued Function Expansions." 17 Jun 2002. https://arxiv.org/abs/math.NT/0206166. 
Page and Part : ...|
Read More
Date: 23-11-2019
1578
Date: 2-4-2020
564
Date: 28-4-2020
640
|
The Bolyai expansion of a real number 
is a nested root of the form
![x=a_0-1+RadicalBox[{{a, _, 1}, +, RadicalBox[{{a, _, 2}, +, RadicalBox[{{a, _, 3}, +, ...}, m]}, m]}, m],](https://mathworld.wolfram.com/images/equations/BolyaiExpansion/NumberedEquation1.gif) |
where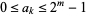 
.
REFERENCES:
Martin, G. "The Unreasonable Effectualness of Continued Function Expansions." 17 Jun 2002. https://arxiv.org/abs/math.NT/0206166.
Rényi, A. "Representations for Real Numbers and Their Ergodic Properties." Acta Math. Acad. Sci. Hungar. 8, 477-493, 1957.
Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, pp. 80-81, 2004. https://www.mathematicaguidebooks.org/.
|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|
