المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر المرجع الالكتروني للمعلوماتية
أضيف حديثاً
معنى قوله تعالى : كَذَلِكَ نَسْلُكُهُ فِي قُلُوبِ الْمُجْرِمِينَ
2025-04-14
معنى قوله تعالى : لَا تَأْكُلُوا أَمْوَالَكُمْ بَيْنَكُمْ بِالْبَاطِلِ
2025-04-14
معنى قوله تعالى : لَا تَمُدَّنَّ عَيْنَيْكَ إِلَى مَا مَتَّعْنَا بِهِ أَزْوَاجًا مِنْهُمْ
2025-04-14
معنى قوله تعالى : لَا جَرَمَ أَنَّهُمْ فِي الْآخِرَةِ هُمُ الْأَخْسَرُونَ
2025-04-14
معنى قوله تعالى : لَا يَرْقُبُوا فِيكُمْ إِلًّا وَلَا ذِمَّةً
2025-04-14
الجهة المختصة في التفاوض والتوقيع
2025-04-14

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024

مختارات
[الجود و حسن الخلق في علي]
22-10-2015
الجهاز العصبي في الحشرات The Nervous System in The Insects
2025-02-21
منبع الحرارة الأرضية عند أبو إسحاق الإصطخري (القرن 4هـ / 10م)
2023-05-18
النبي (ص) واحداث ما قبل حرب بدر
14-6-2021
الدولة المعينية
11-11-2016
عموم التوبة
14/9/2022

Truncated Tetrahedral Number  
  
1084   12:07 صباحاً   date: 25-12-2020
Author : Conway, J. H. and Guy, R. K.
Book or Source : The Book of Numbers. New York: Springer-Verlag,
Page and Part : ...


Read More
Rational Number
Date: 18-10-2020 2351
Landau-Ramanujan Constant
Date: 2-3-2020 941
Random Fibonacci Sequence
Date: 8-12-2020 2499

Truncated Tetrahedral Number

A figurate number constructed by taking the 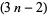(3n-2)th tetrahedral number and removing the 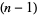(n-1)th tetrahedral number from each of the four corners,

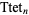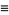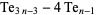Ttet_n = Te_(3n-3)-4Te_(n-1)

(1)
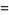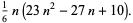= 1/6n(23n^2-27n+10).

(2)

The first few are 1, 16, 68, 180, 375, ... (OEIS A005906). The generating function for the truncated tetrahedral numbers is

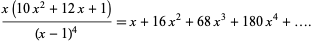(x(10x^2+12x+1))/((x-1)^4)=x+16x^2+68x^3+180x^4+....

(3)

REFERENCES:

Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 46-47, 1996.

Sloane, N. J. A. Sequence A005906/M5002 in "The On-Line Encyclopedia of Integer Sequences."




الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
التاريخ / 2025-04-13

الأخبار العلمية
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
التاريخ / 2025-04-13

الساحة الاسلامية
ملاكات العتبة العباسية المقدسة تُنهي أعمال غسل حرم مرقد أبي الفضل العباس (عليه السلام) وفرشه
التاريخ / 2025-04-14