


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-1-2021
Date: 17-2-2020
Date: 17-12-2019
|
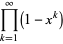 |
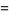 |
 |
(1) |
 |
 |
![1+sum_(k=1)^(infty)(-1)^k[x^(k(3k-1)/2)+x^(k(3k+1)/2)]](https://mathworld.wolfram.com/images/equations/PentagonalNumberTheorem/Inline6.gif) |
(2) |
 |
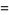 |
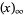 |
(3) |
 |
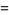 |
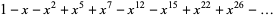 |
(4) |
(OEIS A010815), where 0, 1, 2, 5, 7, 12, 15, 22, 26, ... (OEIS A001318) are generalized pentagonal numbers and 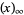 is a q-Pochhammer symbol.
is a q-Pochhammer symbol.
This identity was proved by Euler (1783) in a paper presented to the St. Petersburg Academy on August 14, 1775.
Related equalities are
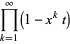 |
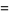 |
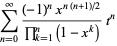 |
(5) |
 |
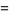 |
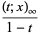 |
(6) |
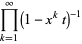 |
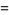 |
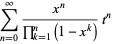 |
(7) |
 |
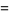 |
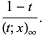 |
(8) |
REFERENCES:
Bailey, W. N. Generalised Hypergeometric Series. Cambridge, England: Cambridge University Press, p. 72, 1935.
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, pp. 221-222, 2007.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, p. 64, 1987.
Euler, L. "Evolutio producti infiniti 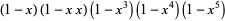 etc. in seriem simplicem." Acta Academiae Scientarum Imperialis Petropolitinae 1780, pp. 47-55, 1783. Opera Omnia, Series Prima, Vol. 3. pp. 472-479. Translated as Bell, J. "The Expansion of the Infinite Product
etc. in seriem simplicem." Acta Academiae Scientarum Imperialis Petropolitinae 1780, pp. 47-55, 1783. Opera Omnia, Series Prima, Vol. 3. pp. 472-479. Translated as Bell, J. "The Expansion of the Infinite Product 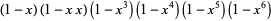 etc. into a Single Series." Dec. 4, 2004. https://www.arxiv.org/abs/math.HO/0411454/.
etc. into a Single Series." Dec. 4, 2004. https://www.arxiv.org/abs/math.HO/0411454/.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, pp. 83-85, 1999.
Sloane, N. J. A. Sequences A001318/M1336 and A010815 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|