k-ary Divisor

Let a divisor 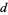 of 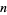 be called a 1-ary (or unitary) divisor if  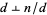(i.e.,  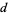is relatively prime to 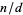). Then  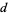is called a 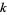-ary divisor of 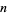, written 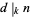, if the greatest common 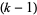-ary divisor of  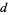and 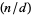 is 1 (Cohen 1990).

In this notation, 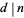 is written 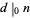, and 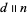 is written .

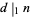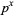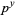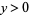 is an infinitary divisor of  (with ) if .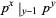

Suryanarayana (1968) unfortunately uses a different and conflicting definition.

REFERENCES:

Abbott, P. "In and Out: 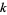-ary Divisors." Mathematica J. 9, 702-706, 2005.

Cohen, G. L. "On an Integer's Infinitary Divisors." Math. Comput. 54, 395-411, 1990.

Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 54, 1994.

Suryanarayana, D. "The Number of 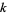-ary Divisors of an Integer." Monatschr. Math. 72, 445-450, 1968.