

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Periodic Continued Fraction
المؤلف:
Liberman, H.
المصدر:
Simple Continued Fractions: An Elementary to Research Level Approach. SMD Stock Analysts, 2003.
الجزء والصفحة:
...
10-5-2020
1101
Periodic Continued Fraction
A periodic continued fraction is a continued fraction (generally a regular continued fraction) whose terms eventually repeat from some point onwards. The minimal number of repeating terms is called the period of the continued fraction. All nontrivial periodic continued fractions represent irrational numbers. In general, an infinite simple fraction (periodic or otherwise) represents a unique irrational number, and each irrational number has a unique infinite continued fraction.
The square root of a squarefree integer has a periodic continued fraction of the form
![sqrt(n)=[a_0;a_1,a_2,a_3,...,a_2,a_1,2a_0^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/NumberedEquation1.gif) |
(1) |
(Rose 1994, p. 130), where the repeating portion (excluding the last term) is symmetric upon reversal, and the central term may appear either once or twice.
If 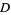 is not a square number, then the terms of the continued fraction of
is not a square number, then the terms of the continued fraction of 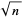 satisfy
satisfy
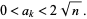 |
(2) |
An even stronger result is that a continued fraction is periodic iff it is a root of a quadratic polynomial. Calling the portion of a number  remaining after a given convergent the "tail," it must be true that the relationship between the number
remaining after a given convergent the "tail," it must be true that the relationship between the number  and terms in its tail is of the form
and terms in its tail is of the form
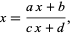 |
(3) |
which can only lead to a quadratic equation.
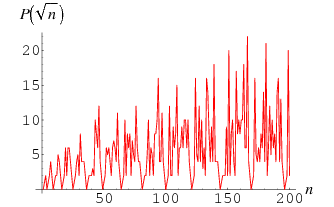
The periods of the continued fractions of the square roots of the first few nonsquare integers 2, 3, 5, 6, 7, 8, 10, 11, 12, 13, ... (OEIS A000037) are 1, 2, 1, 2, 4, 2, 1, 2, 2, 5, ... (OEIS A013943; Williams 1981, Jacobson et al. 1995). These numbers and their continued fraction representations are summarized in the following table.
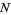 |
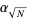 |
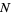 |
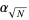 |
| 2 | ![[1,2^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline9.gif) |
22 | ![[4,1,2,4,2,1,8^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline10.gif) |
| 3 | ![[1,1,2^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline11.gif) |
23 | ![[4,1,3,1,8^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline12.gif) |
| 5 | ![[2,4^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline13.gif) |
24 | ![[4,1,8^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline14.gif) |
| 6 | ![[2,2,4^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline15.gif) |
26 | ![[5,10^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline16.gif) |
| 7 | ![[2,1,1,1,4^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline17.gif) |
27 | ![[5,5,10^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline18.gif) |
| 8 | ![[2,1,4^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline19.gif) |
28 | ![[5,3,2,3,10^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline20.gif) |
| 10 | ![[3,6^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline21.gif) |
29 | ![[5,2,1,1,2,10^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline22.gif) |
| 11 | ![[3,3,6^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline23.gif) |
30 | ![[5,2,10^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline24.gif) |
| 12 | ![[3,2,6^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline25.gif) |
31 | ![[5,1,1,3,5,3,1,1,10^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline26.gif) |
| 13 | ![[3,1,1,1,1,6^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline27.gif) |
32 | ![[5,1,1,1,10^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline28.gif) |
| 14 | ![[3,1,2,1,6^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline29.gif) |
33 | ![[5,1,2,1,10^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline30.gif) |
| 15 | ![[3,1,6^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline31.gif) |
34 | ![[5,1,4,1,10^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline32.gif) |
| 17 | ![[4,8^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline33.gif) |
35 | ![[5,1,10^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline34.gif) |
| 18 | ![[4,4,8^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline35.gif) |
37 | ![[6,12^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline36.gif) |
| 19 | ![[4,2,1,3,1,2,8^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline37.gif) |
38 | ![[6,6,12^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline38.gif) |
| 20 | ![[4,2,8^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline39.gif) |
39 | ![[6,4,12^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline40.gif) |
| 21 | ![[4,1,1,2,1,1,8^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline41.gif) |
40 | ![[6,3,12^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline42.gif) |
An upper bound for the length of the period is roughly 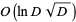 . The least positive
. The least positive 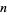 s such that the continued fraction of
s such that the continued fraction of 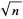 has period
has period 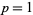 , 2, ... are 2, 3, 41, 7, 13, 19, 58, 31, 106, ... (OEIS A013646). The first few values of
, 2, ... are 2, 3, 41, 7, 13, 19, 58, 31, 106, ... (OEIS A013646). The first few values of 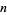 such that the continued fraction of
such that the continued fraction of 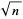 has period
has period 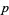 are summarized below for small
are summarized below for small 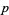 .
.
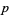 |
OEIS | 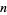 |
| 1 | A002522 | 2, 5, 10, 17, 26, 37, 50, 65, 82, 101, ... |
| 2 | A013642 | 3, 6, 8, 11, 12, 15, 18, 20, 24, 27, ... |
| 3 | A013643 | 41, 130, 269, 370, 458, ... |
| 4 | A013644 | 7, 14, 23, 28, 32, 33, 34, 47, 55, 60, ... |
| 5 | A010337 | 13, 29, 53, 74, 85, 89, 125, 173, 185, 218, ... |
| 6 | A020347 | 19, 21, 22, 45, 52, 54, 57, 59, 70, 77, ... |
| 7 | A010338 | 58, 73, 202, 250, 274, 314, 349, 425, ... |
| 8 | A020348 | 31, 44, 69, 71, 91, 92, 108, 135, 153, 158, ... |
| 9 | A010339 | 106, 113, 137, 149, 265, 389, 493, ... |
| 10 | A020349 | 43, 67, 86, 93, 115, 116, 118, 129, 154, 159, ... |
The values of 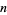 at which the period of the continued fraction of
at which the period of the continued fraction of 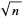 increases are 1, 2, 3, 7, 13, 19, 31, 43, 46, 94, 139, 151, 166, 211, 331, 421, 526, 571, ... (OEIS A013645).
increases are 1, 2, 3, 7, 13, 19, 31, 43, 46, 94, 139, 151, 166, 211, 331, 421, 526, 571, ... (OEIS A013645).
General identities for periodic continued fractions include
![[a^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline55.gif) |
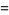 |
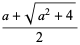 |
(4) |
![[1,a^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline58.gif) |
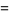 |
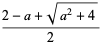 |
(5) |
![[a,2a^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline61.gif) |
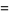 |
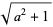 |
(6) |
![[a,b^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline64.gif) |
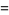 |
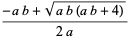 |
(7) |
![[a_1,...,a_n^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline67.gif) |
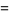 |
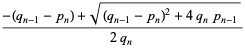 |
(8) |
![[a_0,b_1,...,b_n^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline70.gif) |
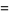 |
![a_0+1/([b_1,...,b_n^_])](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline72.gif) |
(9) |
![[b_1,...,b_n^_]](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline73.gif) |
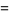 |
![([b_1,...,b_n^_]p_n+p_(n-1))/([b_1,...,b_n^_]q_n+q_(n-1))](https://mathworld.wolfram.com/images/equations/PeriodicContinuedFraction/Inline75.gif) |
(10) |
(Wall 1948, pp. 39 and 83).
The first follows from
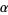 |
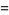 |
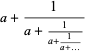 |
(11) |
 |
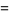 |
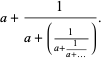 |
(12) |
Therefore,
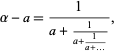 |
(13) |
so plugging (13) into (12) gives
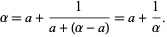 |
(14) |
Expanding
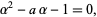 |
(15) |
and solving using the quadratic formula gives
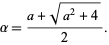 |
(16) |
The analog of this treatment in the general case gives
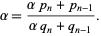 |
(17) |
REFERENCES:
Liberman, H. Simple Continued Fractions: An Elementary to Research Level Approach. SMD Stock Analysts, 2003.
Rose, H. E. A Course in Number Theory, 2nd ed. Oxford, England: Oxford University Press, 1994.
Rosen, K. H. Elementary Number Theory and Its Applications. New York: Addison-Wesley, p. 426, 1980.
Sloane, N. J. A. Sequences A010337, A010338, A010339, A013642, A013643, A013644, A013645, A013646, A020347, A020348, and A020349 in "The On-Line Encyclopedia of Integer Sequences."
Wall, H. S. Analytic Theory of Continued Fractions. New York: Chelsea, 1948.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















