Pentagonal Square Triangular Number

A pentagonal square triangular number is a number that is simultaneously a pentagonal number 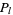, a square number 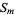, and a triangular number 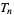. This requires a solution to the system of Diophantine equations

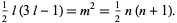Solutions of this system can be searched for by checking pentagonal triangular numbers (for which there is a closed-form solution) up to some limit to see if any are also square. Other than the trivial case 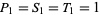, using this approach shows that none of the first 9690 pentagonal triangular numbers are square, thus showing that there is no other pentagonal square triangular number less than  (E. W. Weisstein, Sept. 12, 2003).

It is almost certain, therefore, that no other solution exists, although no proof of this fact appears to have yet appeared in print. However, recent work by J. Sillcox (pers. comm., Nov. 8, 2003 and Feb. 17, 2006) may have finally settled the problem. This work used a paper by Anglin (1996) that proves simultaneous Pell equations 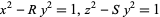 have exactly 19900 solutions with 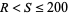. For example, if  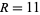and 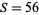, then  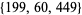is a solution. Sillcox then shows that the pentagonal square triangular number problem is equivalent to solving 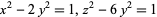, putting it within the bounds of Anglin's proof. For  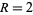and 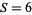, only the trivial solution exists.

REFERENCES:

Anglin, W. S. "Simultaneous Pell Equations." Math. Comput. 65, 355-359, 1996.