


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 8-2-2020
Date: 6-1-2020
Date: 17-11-2019
|
Fractran is an algorithm applied to a given list  ,
, 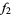 , ...,
, ..., 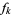 of fractions. Given a starting integer
of fractions. Given a starting integer 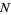 , the FRACTRAN algorithm proceeds by repeatedly multiplying the integer at a given stage by the first element
, the FRACTRAN algorithm proceeds by repeatedly multiplying the integer at a given stage by the first element 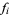 that yields an integer product. The algorithm terminates when there is no such
that yields an integer product. The algorithm terminates when there is no such 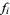 .
.
The list
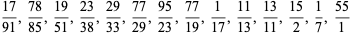 |
with starting integer 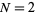 generates a sequence 2, 15, 825, 725, 1925, 2275, 425, 390, 330, 290, 770, ... (OEIS A007542). Conway (1987) showed that this sequence has an amazing connection with prime numbers, and in fact is a generator for the primes. In particular, the only powers of two (other than 2 itself) that occur in this sequence are those with prime exponent:
generates a sequence 2, 15, 825, 725, 1925, 2275, 425, 390, 330, 290, 770, ... (OEIS A007542). Conway (1987) showed that this sequence has an amazing connection with prime numbers, and in fact is a generator for the primes. In particular, the only powers of two (other than 2 itself) that occur in this sequence are those with prime exponent: 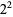 ,
, 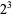 ,
, 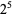 ,
, 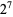 , ....
, ....
REFERENCES:
Conway, J. H. "Unpredictable Iterations." In Proceedings of the 1972 Number Theory Conference Held at the University of Colorado, Boulder, Colo., Aug. 14-18, 1972. Boulder, CO: University of Colorado, pp. 49-52, 1972.
Conway, J. H. "Fractran: A Simple Universal Programming Language for Arithmetic." Ch. 2 in Open Problems in Communication and Computation (Ed. T. M. Cover and B. Gopinath). New York: Springer-Verlag, pp. 4-26, 1987.
Sloane, N. J. A. Sequence A007542/M2084 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|