


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 20-9-2020
Date: 20-9-2020
Date: 18-9-2020
|
PASCAL’S LAW FOR INCOMPRESSIBLE LIQUIDS
Imagine a watertight, rigid container. Suppose that there are two pipes of unequal diameters running upward out of this container. Imagine that you fill the container with an incompressible liquid such as water so that the container is completely full and the water rises partway up into the pipes. Suppose that you place pistons in the pipes so that they make perfect water seals, and then you leave the pistons to rest on the water surface (Fig. 1).
Because the pipes have unequal diameters, the surface areas of the pistons are different. One of the pistons has area A1 (in meters squared), and the other has area A2. Suppose that you push downward on piston number 1 (the one whose area is A1) with a force F1 (in newtons). How much upward force F2 is produced at piston number 2 (the one whose area is A2)? Pascal’s law provides the answer: The forces are directly proportional to the areas of the piston faces in terms of their contact with the liquid. In the example shown by Fig. 1, piston number 2 is smaller than piston number 1, so the force F2 is proportionately less than the force F1. Mathematically, the following equations both hold:
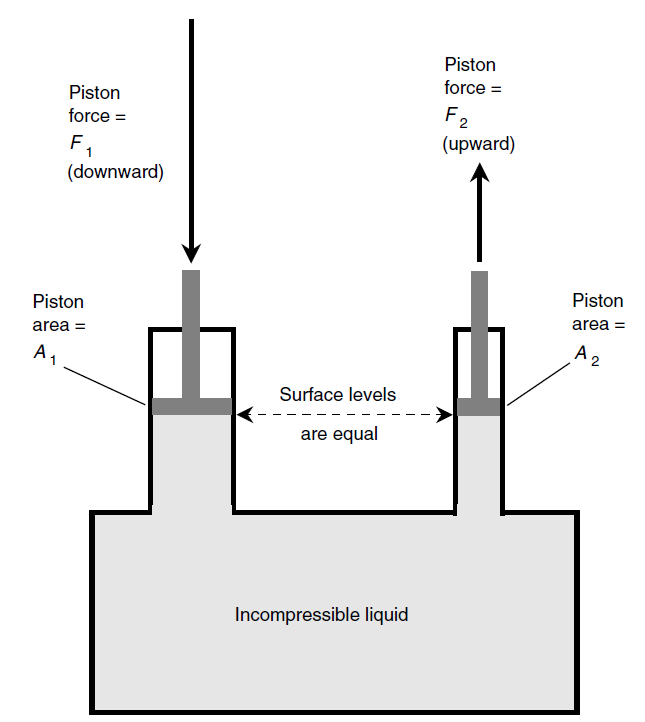
Fig. 1. Pascal’s law for confined, incompressible liquids. The forces are directly proportional to the areas of the pistons.
F1/F2 = A1/A2
A1F2 = A2F1
When using either of these equations, we must be consistent with units throughout the calculations. In addition, the top equation is meaningful only as long as the force exerted is nonzero.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مستشفى العتبة العباسية الميداني في سوريا يقدّم خدماته لنحو 1500 نازح لبناني يوميًا
|
|
|