Elliptic Curve Factorization Method

The elliptic curve factorization method, abbreviated ECM and sometimes also called the Lenstra elliptic curve method, is a factorization algorithm that computes a large multiple of a point on a random elliptic curve modulo the number to be factored 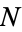. It tends to be faster than the Pollard rho factorization and Pollard p-1 factorization methods.

Zimmermann maintains a table of the largest factors found using the ECM. As of Jan. 2009, the largest prime factor found using the ECM had 67 decimal digits. This factor of 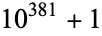 was found by B. Dodson on Aug. 24, 2006 (Zimmermann).

REFERENCES:

Alpern, D. "Factorization Using the Elliptic Curve Method." https://www.alpertron.com.ar/ECM.HTM.

Atkin, A. O. L. and Morain, F. "Finding Suitable Curves for the Elliptic Curve Method of Factorization." Math. Comput. 60, 399-405, 1993.

Brent, R. P. "Some Integer Factorization Algorithms Using Elliptic Curves." Austral. Comp. Sci. Comm. 8, 149-163, 1986.

Brent, R. P. "Parallel Algorithms for Integer Factorisation." In Number Theory and Cryptography (Ed. J. H. Loxton). New York: Cambridge University Press, pp. 26-37, 1990.

Brillhart, J.; Lehmer, D. H.; Selfridge, J.; Wagstaff, S. S. Jr.; and Tuckerman, B. Factorizations of b-n+/-1, b=2, 3, 5, 6, 7, 10, 11, 12 Up to High Powers, rev. ed. Providence, RI: Amer. Math. Soc., p. lxxxiii, 1988.

Eldershaw, C. and Brent, R. P. "Factorization of Large Integers on Some Vector and Parallel Computers." Australian National University, Technical Report TR-CS-95-01. January 1995. https://cs.anu.edu.au/techreports/1995/TR-CS-95-01.html.

Lenstra, A. K. and Lenstra, H. W. Jr. "Algorithms in Number Theory." In Handbook of Theoretical Computer Science, Volume A: Algorithms and Complexity (Ed. J. van Leeuwen). Amsterdam: Netherlands, Elsevier, pp. 673-715, 1990.

Lenstra, H. W. Jr. "Factoring Integers with Elliptic Curves." Ann. Math. 126, 649-673, 1987.

Montgomery, P. L. "Speeding the Pollard and Elliptic Curve Methods of Factorization." Math. Comput. 48, 243-264, 1987.