Small Numbers  (3)

3 is the only integer which is the sum of the preceding positive integers (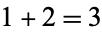) and the only number which is the sum of the factorials of the preceding positive integers (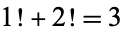). It is also the first odd prime. A quantity taken to the power 3 is said to be cubed.

The sequence 1, 31, 331, 3331, 33331, ... (OEIS A033175) consisting of 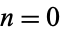, 1, ... 3s followed by a 1 has its 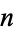th term is given by

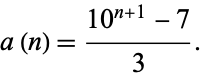The result is prime for 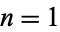, 2, 3, 4, 5, 6, 7, 17, 39, ... (OEIS A055520); i.e., for 31, 331, 3331, 33331, 333331, 3333331, 33333331, ... (OEIS A051200), a fact which Gardner (1997) calls "a remarkable pattern that is entirely accidental and leads nowhere."

REFERENCES:

Gardner, M. The Last Recreations: Hydras, Eggs, and Other Mathematical Mystifications. New York: Springer-Verlag, p. 194, 1997.

Sloane, N. J. A. Sequences A033175, A051200, and A055520 in "The On-Line Encyclopedia of Integer Sequences."

Smarandache, F. Properties of Numbers. University of Craiova, 1973.

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, pp. 46-48, 1986.a