


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-12-2020
Date: 30-4-2020
Date: 26-7-2020
|
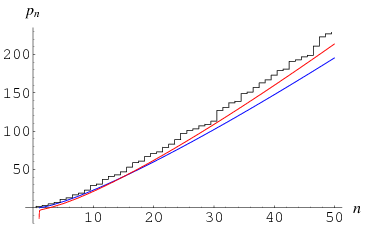
The prime number theorem shows that the 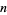 th prime number
th prime number 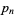 has the asymptotic value
has the asymptotic value
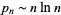 |
(1) |
as 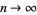 (Havil 2003, p. 182). Rosser's theorem makes this a rigorous lower bound by stating that
(Havil 2003, p. 182). Rosser's theorem makes this a rigorous lower bound by stating that
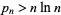 |
(2) |
for 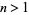 (Rosser 1938). This result was subsequently improved to
(Rosser 1938). This result was subsequently improved to
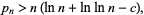 |
(3) |
where 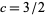 (Rosser and Schoenfeld 1975). The constant
(Rosser and Schoenfeld 1975). The constant 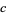 was subsequently reduced to
was subsequently reduced to 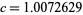 (Robin 1983). Massias and Robin (1996) then showed that
(Robin 1983). Massias and Robin (1996) then showed that 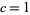 was admissible for
was admissible for 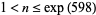 and
and 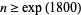 . Finally, Dusart (1999) showed that
. Finally, Dusart (1999) showed that 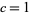 holds for all
holds for all 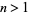 (Havil 2003, p. 183). The plots above show
(Havil 2003, p. 183). The plots above show 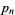 (black),
(black), 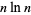 (blue), and
(blue), and 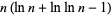 (red).
(red).
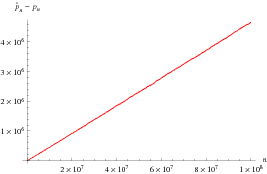
The difference between 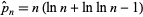 and
and 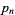 is plotted above. The slope of the difference taken out to
is plotted above. The slope of the difference taken out to 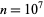 is approximately
is approximately 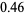 .
.
REFERENCES:
Dusart, P. "The 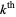 Prime is Greater than
Prime is Greater than 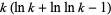 for
for 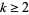 ." Math. Comput. 68, 411-415, 1999.
." Math. Comput. 68, 411-415, 1999.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.
Massias, J.-P. and Robin, G. "Bornes effectives pour certaines fonctions concernant les nombres premiers." J. Théor. Nombres Bordeaux 8, 215-242, 1996.
Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 56-57, 1994.
Robin, G. "Estimation de la fonction de Tschebychef 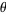 sur le
sur le 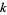 -iéme nombre premier et grandes valeurs de la fonction
-iéme nombre premier et grandes valeurs de la fonction 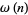 , nombres de diviseurs premiers de
, nombres de diviseurs premiers de 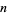 ." Acta Arith. 42, 367-389, 1983.
." Acta Arith. 42, 367-389, 1983.
Robin, G. "Permanence de relations de récurrence dans certains développements asymptotiques." Publ. Inst. Math., Nouv. Sér. 43, 17-25, 1988.
Rosser, J. B. "The 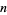 th Prime is Greater than
th Prime is Greater than 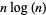 ." Proc. London Math. Soc. 45, 21-44, 1938.
." Proc. London Math. Soc. 45, 21-44, 1938.
Rosser, J. B. and Schoenfeld, L. "Sharper Bounds for Chebyshev Functions 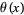 and
and 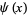 ." Math. Comput. 29, 243-269, 1975.
." Math. Comput. 29, 243-269, 1975.
Salvy, B. "Fast Computation of Some Asymptotic Functional Inverses." J. Symb. Comput. 17, 227-236, 1994.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|