


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-12-2020
Date: 13-8-2020
Date: 25-10-2020
|
Pythagoras's theorem states that the diagonal 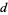 of a square with sides of integral length
of a square with sides of integral length 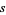 cannot be rational. Assume
cannot be rational. Assume 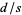 is rational and equal to
is rational and equal to 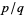 where
where 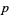 and
and 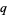 are integers with no common factors. Then
are integers with no common factors. Then
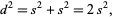 |
so
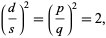 |
and 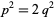 , so
, so 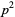 is even. But if
is even. But if 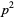 is even, then
is even, then 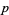 is even. Since
is even. Since 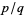 is defined to be expressed in lowest terms,
is defined to be expressed in lowest terms, 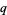 must be odd; otherwise
must be odd; otherwise 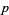 and
and 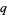 would have the common factor 2. Since
would have the common factor 2. Since 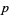 is even, we can let
is even, we can let 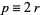 , then
, then 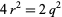 . Therefore,
. Therefore, 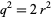 , and
, and 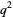 , so
, so 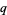 must be even. But
must be even. But 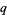 cannot be both even and odd, so there are no
cannot be both even and odd, so there are no 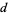 and
and 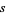 such that
such that 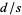 is rational, and
is rational, and 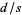 must be irrational.
must be irrational.
In particular, Pythagoras's constant 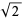 is irrational. Conway and Guy (1996) give a proof of this fact using paper folding, as well as similar proofs for
is irrational. Conway and Guy (1996) give a proof of this fact using paper folding, as well as similar proofs for 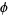 (the golden ratio) and
(the golden ratio) and 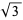 using a pentagon and hexagon. A collection of 17 computer proofs of the irrationality of
using a pentagon and hexagon. A collection of 17 computer proofs of the irrationality of 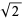 is given by Wiedijk (2006).
is given by Wiedijk (2006).
REFERENCES:
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 183-186, 1996.
Gardner, M. The Sixth Book of Mathematical Games from Scientific American. Chicago, IL: University of Chicago Press, p. 70, 1984.
Pappas, T. "Irrational Numbers & the Pythagoras Theorem." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 98-99, 1989.
Wiedijk, F. (Ed.). The Seventeen Provers of the World. Berlin: Springer-Verlag, 2006.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|