Fermat's Last Theorem

Fermat's last theorem is a theorem first proposed by Fermat in the form of a note scribbled in the margin of his copy of the ancient Greek text Arithmetica by Diophantus. The scribbled note was discovered posthumously, and the original is now lost. However, a copy was preserved in a book published by Fermat's son. In the note, Fermat claimed to have discovered a proof that the Diophantine equation  has no integer solutions for  and .

The full text of Fermat's statement, written in Latin, reads "Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividere cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet" (Nagell 1951, p. 252). In translation, "It is impossible for a cube to be the sum of two cubes, a fourth power to be the sum of two fourth powers, or in general for any number that is a power greater than the second to be the sum of two like powers. I have discovered a truly marvelous demonstration of this proposition that this margin is too narrow to contain."

As a result of Fermat's marginal note, the proposition that the Diophantine equation

(1)

where , , , and  are integers, has no nonzero solutions for  has come to be known as Fermat's Last Theorem. It was called a "theorem" on the strength of Fermat's statement, despite the fact that no other mathematician was able to prove it for hundreds of years.

Note that the restriction  is obviously necessary since there are a number of elementary formulas for generating an infinite number of Pythagorean triples  satisfying the equation for ,

(2)

A first attempt to solve the equation can be made by attempting to factor the equation, giving

(3)

Since the product is an exact power,

(4)

Solving for  and  gives

(5)

which give

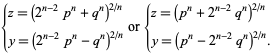(6)

However, since solutions to these equations in rational numbers are no easier to find than solutions to the original equation, this approach unfortunately does not provide any additional insight.

If an odd prime  divides , then the reduction

(7)

can be made, so redefining the arguments gives

(8)

If no odd prime divides , then  is a power of 2, so  and, in this case, equations (7) and (8) work with 4 in place of . Since the case  was proved by Fermat to have no solutions, it is sufficient to prove Fermat's last theorem by considering odd prime powers only.

Similarly, is sufficient to prove Fermat's last theorem by considering only relatively prime , , and , since each term in equation (1) can then be divided by , where  is the greatest common divisor.

The so-called "first case" of the theorem is for exponents which are relatively prime to , , and  () and was considered by Wieferich. Sophie Germain proved the first case of Fermat's Last Theorem for any odd prime  when  is also a prime. Legendre subsequently proved that if  is a prime such that , , , , or  is also a prime, then the first case of Fermat's Last Theorem holds for . This established Fermat's Last Theorem for . In 1849, Kummer proved it for all regular primes and composite numbers of which they are factors (Vandiver 1929, Ball and Coxeter 1987).

The "second case" of Fermat's last theorem is " divides exactly one of , , . Note that  is ruled out by , ,  being relatively prime, and that if  divides two of , , , then it also divides the third, by equation (8).

Kummer's attack led to the theory of ideals, and Vandiver developed Vandiver's criteria for deciding if a given irregular prime satisfies the theorem. In 1852, Genocchi proved that the first case is true for  if  is not an irregular pair. In 1858, Kummer showed that the first case is true if either  or  is an irregular pair, which was subsequently extended to include  and  by Mirimanoff (1909). Vandiver (1920ab) pointed out gaps and errors in Kummer's memoir which, in his view, invalidate Kummer's proof of Fermat's Last Theorem for the irregular primes 37, 59, and 67, although he claims Mirimanoff's proof of FLT for exponent 37 is still valid.

Wieferich (1909) proved that if the equation is solved in integers relatively prime to an odd prime , then

(9)

(Ball and Coxeter 1987). Such numbers are called Wieferich primes. Mirimanoff (1909) subsequently showed that

(10)

must also hold for solutions relatively prime to an odd prime , which excludes the first two Wieferich primes 1093 and 3511. In 1914, Vandiver showed

(11)

and Frobenius extended this to

(12)

It has also been shown that if  were a prime of the form , then

(13)

which raised the smallest possible  in the "first case" to  by 1941 (Rosser 1941). Granville and Monagan (1988) showed if there exists a prime  satisfying Fermat's Last Theorem, then

(14)

for , 7, 11, ..., 71. This establishes that the first case is true for all prime exponents up to  (Vardi 1991).

The "second case" of Fermat's Last Theorem (for ) proved harder than the first case.

Euler proved the general case of the theorem for , Fermat , Dirichlet and Lagrange . In 1832, Dirichlet established the case . The  case was proved by Lamé (1839; Wells 1986, p. 70), using the identity

(15)

Although some errors were present in this proof, these were subsequently fixed by Lebesgue in 1840. Much additional progress was made over the next 150 years, but no completely general result had been obtained. Buoyed by false confidence after his proof that pi is transcendental, the mathematician Lindemann proceeded to publish several proofs of Fermat's Last Theorem, all of them invalid (Bell 1937, pp. 464-465). A prize of  German marks, known as the Wolfskehl Prize, was also offered for the first valid proof (Ball and Coxeter 1987, p. 72; Barner 1997; Hoffman 1998, pp. 193-194 and 199).

A recent false alarm for a general proof was raised by Y. Miyaoka (Cipra 1988) whose proof, however, turned out to be flawed. Other attempted proofs among both professional and amateur mathematicians are discussed by vos Savant (1993), although vos Savant erroneously claims that work on the problem by Wiles (discussed below) is invalid. By the time 1993 rolled around, the general case of Fermat's Last Theorem had been shown to be true for all exponents up to  (Cipra 1993). However, given that a proof of Fermat's Last Theorem requires truth for all exponents, proof for any finite number of exponents does not constitute any significant progress towards a proof of the general theorem (although the fact that no counterexamples were found for this many cases is highly suggestive).

In 1993, a bombshell was dropped. In that year, the general theorem was partially proven by Andrew Wiles (Cipra 1993, Stewart 1993) by proving the semistable case of the Taniyama-Shimura conjecture. Unfortunately, several holes were discovered in the proof shortly thereafter when Wiles' approach via the Taniyama-Shimura conjecture became hung up on properties of the Selmer group using a tool called an Euler system. However, the difficulty was circumvented by Wiles and R. Taylor in late 1994 (Cipra 1994, 1995) and published in Taylor and Wiles (1995) and Wiles (1995). Wiles' proof succeeds by (1) replacing elliptic curves with Galois representations, (2) reducing the problem to a class number formula, (3) proving that formula, and (4) tying up loose ends that arise because the formalisms fail in the simplest degenerate cases (Cipra 1995).

The proof of Fermat's Last Theorem marks the end of a mathematical era. Since virtually all of the tools which were eventually brought to bear on the problem had yet to be invented in the time of Fermat, it is interesting to speculate about whether he actually was in possession of an elementary proof of the theorem. Judging by the tenacity with which the problem resisted attack for so long, Fermat's alleged proof seems likely to have been illusionary. This conclusion is further supported by the fact that Fermat searched for proofs for the cases  and , which would have been superfluous had he actually been in possession of a general proof.

In the  episode of the television program The Simpsons, the equation  appeared at one point in the background. Expansion reveals that only the first 9 decimal digits match (Rogers 2005). The episode The Wizard of Evergreen Terrace mentions , which matches not only in the first 10 decimal places but also the easy-to-check last place (Greenwald). At the start of Star Trek: The Next Generation episode "The Royale," Captain Picard mentions that studying Fermat's Last Theorem is a relaxing process.

REFERENCES:

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 69-73, 1987.

Barner, K. "Paul Wolfskehl and the Wolfskehl Prize." Not. Amer. Math. Soc. 44, 1294-1303, 1997.

Beiler, A. H. "The Stone Wall." Ch. 24 in Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. New York: Dover, 1966.

Bell, E. T. Men of Mathematics. New York: Simon and Schuster, 1937.

Bell, E. T. The Last Problem. New York: Simon and Schuster, 1961.

Cipra, B. A. "Fermat Theorem Proved." Science 239, 1373, 1988.

Cipra, B. A. "Mathematics--Fermat's Last Theorem Finally Yields." Science 261, 32-33, 1993.

Cipra, B. A. "Is the Fix in on Fermat's Last Theorem?" Science 266, 725, 1994.

Cipra, B. A. "Princeton Mathematician Looks Back on Fermat Proof." Science 268, 1133-1134, 1995.

Cipra, B. A. "Fermat's Theorem--At Last." What's Happening in the Mathematical Sciences, 1995-1996, Vol. 3. Providence, RI: Amer. Math. Soc., pp. 2-14, 1996.

Courant, R. and Robbins, H. "Pythagorean Numbers and Fermat's Last Theorem." §2.3 in Supplement to Ch. 1 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 40-42, 1996.

Cox, D. A. "Introduction to Fermat's Last Theorem." Amer. Math. Monthly 101, 3-14, 1994.

Darmon, H. and Merel, L. "Winding Quotients and Some Variants of Fermat's Last Theorem." J. reine angew. Math. 490, 81-100, 1997.

Dickson, L. E. "Fermat's Last Theorem, 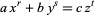, and the Congruence  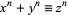(mod 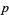)." Ch. 26 in History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Dover, pp. 731-776, 2005.

Edwards, H. M. Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory. New York: Springer-Verlag, 1977.

Edwards, H. M. "Fermat's Last Theorem." Sci. Amer. 239, 104-122, Oct. 1978.

Granville, A. "Review of BBC's Horizon Program, 'Fermat's Last Theorem.' " Not. Amer. Math. Soc. 44, 26-28, 1997.

Granville, A. and Monagan, M. B. "The First Case of Fermat's Last Theorem is True for All Prime Exponents up to 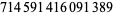." Trans. Amer. Math. Soc. 306, 329-359, 1988.

Greenwald, S. "Dr. Sarah's Futurama 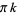--Mathematics in the Year 3000." https://www.mathsci.appstate.edu/~sjg/futurama/.

Guy, R. K. "The Fermat Problem." §D2 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 144-146, 1994.

Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. New York: Hyperion, pp. 183-199, 1998.

Jones, G. A. and Jones, J. M. "Fermat's Last Theorem." Ch. 11 in Elementary Number Theory. Berlin: Springer-Verlag, pp. 217-237, 1998.

Kolata, G. "Andrew Wiles: A Math Whiz Battles 350-Year-Old Puzzle." New York Times, June 29, 1993.

Lynch, J. "Fermat's Last Theorem." BBC Horizon television documentary. https://www.bbc.co.uk/horizon/fermat.shtml.

Lynch, J. (Producer and Writer). "The Proof." NOVA television episode. 52 mins. Broadcast by the U. S. Public Broadcasting System on Oct. 28, 1997.

Mirimanoff, D. "Sur le dernier théorème de Fermat et le critérium de Wiefer." Enseignement Math. 11, 455-459, 1909.

Mordell, L. J. Three lectures on Fermat's Last Theorem. New York: Chelsea, 1956.

Murty, V. K. (Ed.). Fermat's Last Theorem: Proceedings of the Fields Institute for Research in Mathematical Sciences on Fermat's Last Theorem, Held 1993-1994 Toronto, Ontario, Canada. Providence, RI: Amer. Math. Soc., 1995.

Nagell, T. "Fermat's Last Theorem." §68 in Introduction to Number Theory. New York: Wiley, pp. 251-253, 1951.

Osserman, R. (Ed.). Fermat's Last Theorem. The Theorem and Its Proof: An Exploration of Issues and Ideas. 98 min. videotape and 56 pp. book. 1994.

Ribenboim, P. 13 Lectures on Fermat's Last Theorem. New York: Springer-Verlag, 1979.

Ribenboim, P. Fermat's Last Theorem for Amateurs. New York: Springer-Verlag, 1999.

Ribet, K. A. "From the Taniyama-Shimura Conjecture to Fermat's Last Theorem." Ann. Fac. Sci. Toulouse Math. 11, 116-139, 1990.

Ribet, K. A. and Hayes, B. "Fermat's Last Theorem and Modern Arithmetic." Amer. Sci. 82, 144-156, March/April 1994.

Ribet, K. A. and Hayes, B. Correction to "Fermat's Last Theorem and Modern Arithmetic." Amer. Sci. 82, 205, May/June 1994.

Rogers, D. "Homer Math Catches Up with the News." San Francisco Chronicle, p. B-7. Dec. 16, 2005. https://www.sfgate.com/cgi-bin/article.cgi?file=/chronicle/archive/2005/12/16/EDG7RG8FGG1.DTL.

Rosser, B. "On the First Case of Fermat's Last Theorem." Bull. Amer. Math. Soc. 45, 636-640, 1939.

Rosser, B. "A New Lower Bound for the Exponent in the First Case of Fermat's Last Theorem." Bull. Amer. Math. Soc. 46, 299-304, 1940.

Rosser, B. "An Additional Criterion for the First Case of Fermat's Last Theorem." Bull. Amer. Math. Soc. 47, 109-110, 1941.

Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 144-149, 1993.

Shay, D. "Fermat's Last Theorem." https://fermat.workjoke.com/.

Singh, S. Fermat's Enigma: The Quest to Solve the World's Greatest Mathematical Problem. New York: Walker & Co., 1997.

Stewart, I. "Fermat's Last Time-Trip." Sci. Amer. 269, 112-115, 1993.

Stewart, I. and Tall, D. Algebraic Number Theory and Fermat's Last Theorem, 3rd ed. Wellesley, MA: A K Peters, 2000.

Swinnerton-Dwyer, P. Nature 364, 13-14, 1993.

Taylor, R. and Wiles, A. "Ring-Theoretic Properties of Certain Hecke Algebras." Ann. Math. 141, 553-572, 1995.

van der Poorten, A. Notes on Fermat's Last Theorem. New York: Wiley, 1996.

Vandiver, H. S. "On Kummer's Memoir of 1857 Concerning Fermat's Last Theorem." Proc. Nat. Acad. Sci. 6, 266-269, 1920a.

Vandiver, H. S. "On the Class Number of the Field 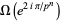 and the Second Case of Fermat's Last Theorem." Proc. Nat. Acad. Sci. 6, 416-421, 1920b.

Vandiver, H. S. "On Fermat's Last Theorem." Trans. Amer. Math. Soc. 31, 613-642, 1929.

Vandiver, H. S. Fermat's Last Theorem and Related Topics in Number Theory. Ann Arbor, MI: 1935.

Vandiver, H. S. "Fermat's Last Theorem: Its History and the Nature of the Known Results Concerning It." Amer. Math. Monthly, 53, 555-578, 1946.

Vandiver, H. S. "A Supplementary Note to a 1946 Article on Fermat's Last Theorem." Amer. Math. Monthly 60, 164-167, 1953.

Vandiver, H. S. "Examination of Methods of Attack on the Second Case of Fermat's Last Theorem." Proc. Nat. Acad. Sci. 40, 732-735, 1954.

Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 59-61, 1991.

vos Savant, M. The World's Most Famous Math Problem. New York: St. Martin's Press, 1993.

Weisstein, E. W. "Books about Fermat's Last Theorem." https://www.ericweisstein.com/encyclopedias/books/FermatsLastTheorem.html.

Wieferich, A. "Zum letzten Fermat'schen Theorem." J. reine angew. Math. 136, 293-302, 1909.

Wiles, A. "Modular Elliptic-Curves and Fermat's Last Theorem." Ann. Math. 141, 443-551, 1995.