


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-3-2020
Date: 24-7-2020
Date: 28-1-2021
|
The term "continued fraction" is used to refer to a class of expressions of which generalized continued fraction of the form
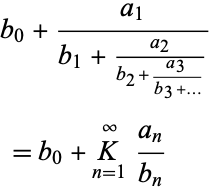 |
(and the terms may be integers, reals, complexes, or functions of these) are the most general variety (Rocket and Szüsz 1992, p. 1).
Wallis first used the term "continued fraction" in his Arithmetica infinitorum of 1653 (Havil 2003, p. 93), although other sources list the publication date as 1655 or 1656. An archaic word for a continued fraction is anthyphairetic ratio.
The simple continued fraction takes 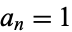 for all
for all 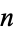 , leaving
, leaving
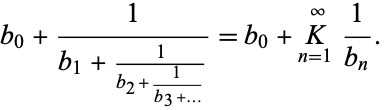 |
If 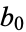 is an integer and the remainder of the partial denominators
is an integer and the remainder of the partial denominators 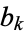 for
for 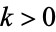 are positive integers, the continued fraction is known as a regular continued fraction.
are positive integers, the continued fraction is known as a regular continued fraction.
REFERENCES:
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.
Rockett, A. M. and Szüsz, P. Continued Fractions. New York: World Scientific, 1992.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
المجمع العلمي يواصل إقامة دوراته القرآنية لطلبة العلوم الدينية في النجف الأشرف
|
|
|