المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Silverman Constant |
 786
 04:27 مساءً
date: 21-3-2020 |
Author : Finch, S. 
Book or Source : "Series Involving Arithmetic Functions." Jan. 24, 2007. http://algo.inria.fr/csolve/arth.pdf. 
Page and Part : ...|
Read More
Date: 14-10-2020
902
Date: 17-12-2019
883
Date: 11-8-2020
756
|
 |
 |
 |
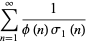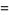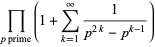(1) |
 |
 |
 |
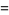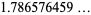(2) |
(OEIS A093827), where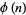 
is the totient function and 
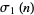is the divisor function.
REFERENCES:
Finch, S. "Series Involving Arithmetic Functions." Jan. 24, 2007. http://algo.inria.fr/csolve/arth.pdf.
Rusin, D. "Re: A Peculiar Sum" In The Mathematical Atlas. http://www.math.niu.edu/~rusin/known-math/96/numtheor.series.
Sloane, N. J. A. Sequence A093827 in "The On-Line Encyclopedia of Integer Sequences."
Zimmermann, P. "Re: A Peculiar Sum." http://algo.inria.fr/csolve/zimmermn.html.
|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
أصواتٌ قرآنية واعدة .. أكثر من 80 برعماً يشارك في المحفل القرآني الرمضاني بالصحن الحيدري الشريف
|
|
|
