Gregory Series

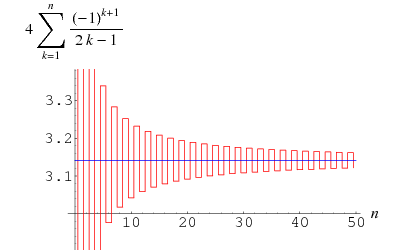
The Gregory series is a pi formula found by Gregory and Leibniz and obtained by plugging 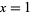 into the Leibniz series,

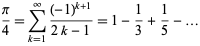(1)

(Wells 1986, p. 50). The formula converges very slowly, but its convergence can be accelerated using certain transformations, in particular

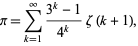(2)

where 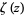 is the Riemann zeta function (Vardi 1991).

Taking the partial series gives the analytic result

(3)

Rather amazingly, expanding about infinity gives the series

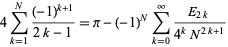(4)

(Borwein and Bailey 2003, p. 50), where 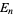 is an Euler number. This means that truncating the Gregory series at half a large power of 10 can give a decimal expansion for  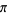whose decimal digits are largely correct, but where wrong digits occur with precise regularity. For example, taking  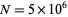gives

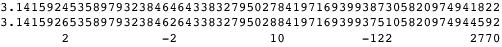
where the sequence of differences is precisely twice the Euler (secant) numbers. In fact, just this pattern of digits was observed by J. R. North in 1988 before the closed form of the truncated series was known (Borwein and Bailey 2003, p. 49; Borwein et al. 2004, p. 29).

REFERENCES:

Borwein, J. and Bailey, D. "A Curious Anomaly in the Gregory Series." §2.2 in Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, pp. 48-50, 2003.

Borwein, J.; Bailey, D.; and Girgensohn, R. "Gregory's Series Reexamined." §1.8.1 in Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, pp. 28-30, 2004.

Borwein, J. M.; Borwein, P. B.; and Dilcher, K. "Pi, Euler Numbers, and Asymptotic Expansions." Amer. Math. Monthly 96, 681-687, 1989.

Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 157-158, 1991.

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 50, 1986.