Strong Lucas Pseudoprime

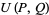Let  and 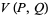 be Lucas sequences generated by  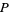and 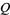, and define

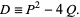(1)

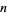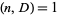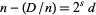Let  be an odd composite number with , and  with 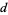 odd and 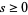, where  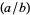is the Legendre symbol. If

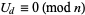(2)

or

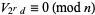(3)

for some 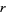 with 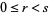, then  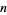is called a strong Lucas pseudoprime with parameters .

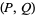A strong Lucas pseudoprime is a Lucas pseudoprime to the same base. Arnault (1997) showed that any composite number 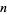 is a strong Lucas pseudoprime for at most 4/15 of possible bases (unless  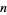is the product of twin primes having certain properties).

REFERENCES:

Arnault, F. "The Rabin-Monier Theorem for Lucas Pseudoprimes." Math. Comput. 66, 869-881, 1997.

Ribenboim, P. "Euler-Lucas Pseudoprimes (elpsp(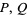)) and Strong Lucas Pseudoprimes (slpsp(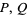))." §2.X.C in The New Book of Prime Number Records, 3rd ed. New York: Springer-Verlag, pp. 130-131, 1996.