


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 3-10-2020
Date: 2-9-2020
Date: 21-9-2020
|
The natural logarithm of 2 is a transcendental quantity that arises often in decay problems, especially when half-lives are being converted to decay constants. 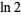 has numerical value
has numerical value
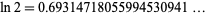 |
(1) |
(OEIS A002162).
The irrationality measure of  is known to be less than 3.8913998 (Rukhadze 1987, Hata 1990).
is known to be less than 3.8913998 (Rukhadze 1987, Hata 1990).
It is not known if  is normal (Bailey and Crandall 2002).
is normal (Bailey and Crandall 2002).
The alternating series and BBP-type formula
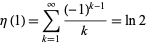 |
(2) |
converges to the natural logarithm of 2, where 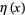 is the Dirichlet eta function. This identity follows immediately from setting
is the Dirichlet eta function. This identity follows immediately from setting 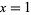 in the Mercator series, yielding
in the Mercator series, yielding
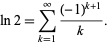 |
(3) |
It is also a special case of the identity
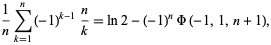 |
(4) |
where 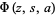 is the Lerch transcendent.
is the Lerch transcendent.
This is the simplest in an infinite class of such identities, the first few of which are
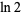 |
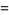 |
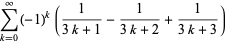 |
(5) |
 |
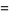 |
 |
(6) |
(E. W. Weisstein, Oct. 7, 2007).
There are many other classes of BBP-type formulas for 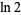 , including
, including
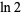 |
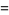 |
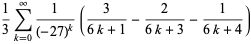 |
(7) |
 |
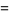 |
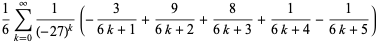 |
(8) |
 |
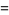 |
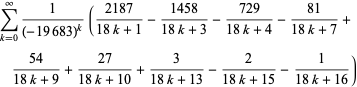 |
(9) |
 |
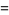 |
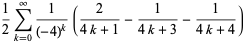 |
(10) |
 |
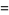 |
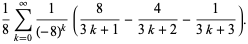 |
(11) |
Plouffe (2006) found the beautiful sum
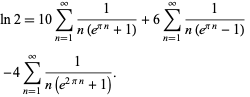 |
(12) |
A rapidly converging Zeilberger-type sum due to A. Lupas is given by
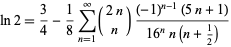 |
(13) |
(Lupas 2000; typos corrected).
The following integral is given in terms of 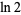 ,
,
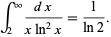 |
(14) |
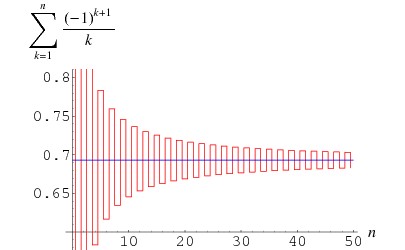
The plot above shows the result of truncating the series for 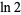 after
after 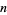 terms.
terms.
Taking the partial series gives the analytic result
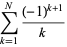 |
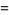 |
![ln2+1/2(-1)^N[psi_0(1/2(N+1))-psi_0(1+1/2N)]](http://mathworld.wolfram.com/images/equations/NaturalLogarithmof2/Inline34.gif) |
(15) |
 |
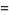 |
![ln2+1/2(-1)^N[H_((N-1)/2)-H_(N/2)],](http://mathworld.wolfram.com/images/equations/NaturalLogarithmof2/Inline37.gif) |
(16) |
where 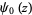 is the digamma function and
is the digamma function and 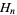 is a harmonic number. Rather amazingly, expanding about infinity gives the series
is a harmonic number. Rather amazingly, expanding about infinity gives the series
![sum_(k=1)^N((-1)^(k+1))/k=ln2+(-1)^N[1/(2N)+sum_(k=0)^infty((-1)^kT_k)/(4^kN^(2k))]](http://mathworld.wolfram.com/images/equations/NaturalLogarithmof2/NumberedEquation8.gif) |
(17) |
(Borwein and Bailey 2002, p. 50), where 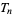 is a tangent number. This means that truncating the series for
is a tangent number. This means that truncating the series for 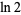 at half a large power of 10 can give a decimal expansion for
at half a large power of 10 can give a decimal expansion for 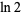 whose decimal digits are largely correct, but where wrong digits occur with precise regularity.
whose decimal digits are largely correct, but where wrong digits occur with precise regularity.
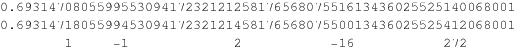
For example, taking 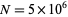 gives a decimal value equal to the second row of digits above, where the sequence of differences from the decimal digits of
gives a decimal value equal to the second row of digits above, where the sequence of differences from the decimal digits of 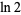 in the top row is precisely the tangent numbers with alternating signs (Borwein and Bailey 2002, p. 49).
in the top row is precisely the tangent numbers with alternating signs (Borwein and Bailey 2002, p. 49).
Beautiful BBP-type formulas for 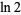 are given by
are given by
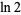 |
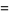 |
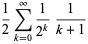 |
(18) |
 |
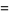 |
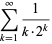 |
(19) |
(Bailey et al. 2007, p. 31) and
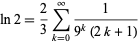 |
(20) |
(Borwein and Bailey 2002, p. 129).
A BBP-type formula for 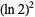 discovered using the PSLQ algorithm is
discovered using the PSLQ algorithm is
![(ln2)^2=1/(32)sum_(k=0)^infty1/(64^k)[(64)/((6k+1)^2)-(160)/((6k+2)^2)-(56)/((6k+3)^2)-(40)/((6k+4)^2)+4/((6k+5)^2)-1/((6k+6)^2)]](http://mathworld.wolfram.com/images/equations/NaturalLogarithmof2/NumberedEquation10.gif) |
(21) |
(Bailey and Plouffe 1997; Borwein and Bailey 2002, p. 128).
The sum
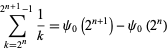 |
(22) |
has the limit
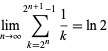 |
(23) |
(Borwein et al. 2004, p. 10).
REFERENCES:
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. "Integer Relation Detection." §2.2 in Experimental Mathematics in Action. Wellesley, MA: A K Peters, pp. 29-31, 2007.
Bailey, D. H.; Borwein, P. B.; and Plouffe, S. "On the Rapid Computation of Various Polylogarithmic Constants." Math. Comput. 66, 903-913, 1997.
Bailey, D. H. and Crandall, R. E. "Random Generators and Normal Numbers." Exper. Math. 11, 527-546, 2002.
Bailey, D. and Plouffe, S. "Recognizing Numerical Constants." Organic Mathematics. Proceedings of the Workshop Held in Burnaby, BC, December 12-14, 1995 (Ed. J. Borwein, P. Borwein, L. Jörgenson, and R. Corless). Providence, RI: Amer. Math. Soc., pp. 73-88, 1997. http://www.cecm.sfu.ca/organics/papers/bailey/.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, 2004.
Gourdon, X. and Sebah, P. "The Constant 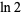 ." http://numbers.computation.free.fr/Constants/Log2/log2.html.
." http://numbers.computation.free.fr/Constants/Log2/log2.html.
Hata, M. "Legendre Type Polynomials and Irrationality Measures." J. reine angew. Math. 407, 99-125, 1990.
Huylebrouck, D. "Similarities in Irrationality Proofs for 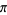 ,
, 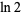 ,
, 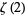 , and
, and 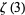 ." Amer. Math. Monthly 108, 222-231, 2001.
." Amer. Math. Monthly 108, 222-231, 2001.
Lupas, A. "Formulae for Some Classical Constants." In Proceedings of ROGER-2000. 2000. http://www.lacim.uqam.ca/~plouffe/articles/alupas1.pdf.
Plouffe, S. "Identities Inspired from Ramanujan Notebooks (Part 2)." Apr. 2006. http://www.lacim.uqam.ca/~plouffe/inspired2.pdf.
Rukhadze, E. A. "A Lower Bound for the Rational Approximation of 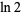 by Rational Numbers." Vestnik Moskov Univ. Ser. I Math. Mekh., No. 6, 25-29 and 97, 1987. [Russian].
by Rational Numbers." Vestnik Moskov Univ. Ser. I Math. Mekh., No. 6, 25-29 and 97, 1987. [Russian].
Sloane, N. J. A. Sequences A002162/M4074, A016730, and A059180 in "The On-Line Encyclopedia of Integer Sequences."
Sweeney, D. W. "On the Computation of Euler's Constant." Math. Comput. 17, 170-178, 1963.
Uhler, H. S. "Recalculation and Extension of the Modulus and of the Logarithms of 2, 3, 5, 7 and 17." Proc. Nat. Acad. Sci. U.S.A. 26, 205-212, 1940.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
ملاكات العتبة العباسية المقدسة تُنهي أعمال غسل حرم مرقد أبي الفضل العباس (عليه السلام) وفرشه
|
|
|