


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 4-3-2020
Date: 19-8-2020
Date: 20-10-2020
|
Let 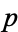 be a prime with
be a prime with 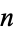 digits and let
digits and let 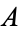 be a constant. Call
be a constant. Call 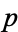 an "
an "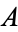 -prime" if the concatenation of the first
-prime" if the concatenation of the first 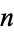 digits of
digits of 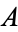 (ignoring the decimal point if one is present) give
(ignoring the decimal point if one is present) give 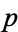 . Constant primes are therefore a special type of integer sequence primes, with e-primes, pi-primes, and phi-primes being perhaps the most prominent examples.
. Constant primes are therefore a special type of integer sequence primes, with e-primes, pi-primes, and phi-primes being perhaps the most prominent examples.
The following table summarizes the indices of known constant primes for some named mathematical constants.
| constant | name of primes | 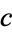 |
OEIS | 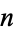 giving prime giving prime |
| Apéry's constant | 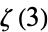 |
A119334 | 10, 55, 109, 141 | |
| Catalan's constant | 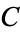 |
A118328 | 52, 276, 25477 | |
| Champernowne constant | 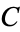 |
A071620 | 10, 14, 24, 235, 2804, 4347, 37735, 68433 | |
| Copeland-Erdős constant | 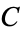 |
A227530 | 1, 2, 4, 11, 353, 355, 499, 1171, 1543, 5719, 11048 | |
| e | e-prime | 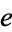 |
A064118 | 1, 3, 7, 85, 1781, 2780, 112280, 155025 |
| Euler-Mascheroni constant | 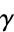 |
A065815 | 1, 3, 40, 185, 1038, 22610, 179849 | |
| Glaisher-Kinkelin constant | 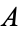 |
A118420 | 7, 10, 18, 64, 71, 527, 1992, 5644, 8813, 19692 | |
| Golomb-Dickman constant | 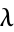 |
A174974 | 6, 27, 57, 60, 1659, 2508 | |
| golden ratio | phi-prime | 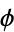 |
A064119 | 7, 13, 255, 280, 97241 |
| Khinchin's constant | 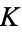 |
A118327 | 1, 407, 878, 4443, 4981, 6551, 13386, 28433 | |
| natural logarithm of 2 | 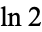 |
A228226 | 321, 466, 1271, 15690, 18872, 89973 | |
| natural logarithm of 10 | 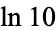 |
A228240 | 1, 2, 40, 242, 842, 1541, 75067 | |
| pi | pi-prime | 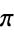 |
A060421 | 2, 6, 38, 16208, 47577, 78073, 613373 |
| Pythagoras's constant | 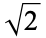 |
A115377 | 55, 97, 225, 11260, 11540 | |
| Soldner's constant | 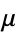 |
A122422 | 4, 144, 227, 444, 19474 | |
| Theodorus's constant | 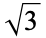 |
A119344 | 2, 3, 19, 111, 116, 641, 5411, 170657 |
The following table summarizes discoverers and discovery dates for some large constant primes.
| constant | digits | discoverer |
| Apéry's constant | 19692 | E. W. Weisstein (Apr. 29, 2006) |
| Champernowne constant | 37735 | E. W. Weisstein (Jul. 15, 2013) |
| Copeland-Erdős constant | 11048 | E. W. Weisstein (Jul. 14, 2013) |
| Copeland-Erdős constant | 68433 | E. W. Weisstein (Aug. 16, 2013) |
| Copeland-Erdős constant | 97855 | E. W. Weisstein (Oct. 24, 2015) |
| Copeland-Erdős constant | 292447 | M. Rodenkirch (Dec. 11, 2015) |
| e | 112280 | E. W. Weisstein (Jul. 3, 2009) |
| e | 155025 | E. W. Weisstein (Oct. 7, 2010) |
| Euler-Mascheroni constant | 22610 | E. W. Weisstein (Apr. 25, 2006) |
| Euler-Mascheroni constant | 179849 | E. W. Weisstein (Jun. 1, 2011) |
| Khinchin's constant | 13386 | E. W. Weisstein (Apr. 26, 2006) |
| Khinchin's constant | 28433 | E. W. Weisstein (Apr. 27, 2006) |
| natural logarithm of 2 | 15690 | E. W. Weisstein (Aug. 17, 2013) |
| natural logarithm of 2 | 18872 | E. W. Weisstein (Aug. 18, 2013) |
| natural logarithm of 2 | 89973 | E. W. Weisstein (Oct. 28, 2015) |
| natural logarithm of 10 | 75067 | E. W. Weisstein (Oct. 10, 2015) |
| pi | 47577 | E. W. Weisstein (Apr. 1, 2006) |
| pi | 16208 | E. W. Weisstein (Jan. 18, 2006) |
| pi | 78073 | E. W. Weisstein (Jul. 13, 2006) |
| pi | 613373 | A. Bondrescu (May 29, 2016) |
| golden ratio | 97289 | E. W. Weisstein (Jun. 4, 2009) |
| Pythagoras's constant | 11260 | E. W. Weisstein (Jan. 21, 2006) |
| Pythagoras's constant | 11540 | E. W. Weisstein (Jan. 21, 2006) |
| Theodorus's constant | 170657 | E. W. Weisstein (Aug. 18, 2013) |
The following table summarizes the values of known constant primes for some named mathematical constants. The first of the 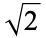 -primes (where
-primes (where 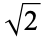 is Pythagoras's constant) was found by J. Earls (Pickover 2002, p. 334) and, contrary to Pickover's claim, is actually the smallest (rather than the largest known) example.
is Pythagoras's constant) was found by J. Earls (Pickover 2002, p. 334) and, contrary to Pickover's claim, is actually the smallest (rather than the largest known) example.
| constant | 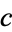 |
OEIS | primes |
| Apéry's constant | 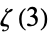 |
A119333 | 1202056903, 1202056903159594285399738161511449990764986292340498881, ... |
| Champernowne constant | 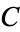 |
A176942 | 1234567891, 12345678910111, 123456789101112131415161, ... |
| Catalan's constant | 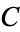 |
A118329 | 9159655941772190150546035149323841107741493742816721, ... |
| Copeland-Erdős constant | 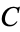 |
A227529 | 2, 23, 2357, 23571113171, ..., |
| e | 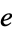 |
A007512 | 2, 271, 2718281, ... |
| Euler-Mascheroni constant | 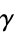 |
A072952 | 5, 577, 5772156649015328606065120900824024310421, ... |
| Glaisher-Kinkelin constant | 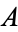 |
A118419 | 1282427, 1282427129, 128242712910062263, ... |
| Golomb-Dickman constant | 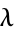 |
A174975 | 624329, 624329988543550870992936383, ... |
| golden ratio | 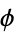 |
A064117 | 1618033, 1618033988749, ... |
| natural logarithm of 10 | 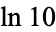 |
A228241 | 2, 23, 2302585092994045684017991454684364207601, ... |
| pi | 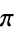 |
A005042 | 3, 31, 314159, 31415926535897932384626433832795028841, ... |
| Pythagoras's constant | 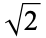 |
A115453 | 1414213562373095048801688724209698078569671875376948073, ... |
| Soldner's constant | 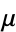 |
A122422 | 1451, ... |
| Theodorus's constant | 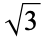 |
A119343 | 17, 173, 1732050807568877293, ... |
REFERENCES:
Pickover, C. A. The Mathematics of Oz: Mental Gymnastics from Beyond the Edge. New York: Cambridge University Press, 2002.
Sloane, N. J. A. Sequences A005042, A007512, A060421, A064117, A064118, A064119, A065815, A071620, A072952, A115377, A115453, A118327, A118328, A118329, A118419, A118420, A119333, A119334, A119343, A119344, A122421, A122422, A174974, A174975, A176942, A227529, A227530, A228226, A228240, and A228241 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|