


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-1-2020
Date: 1-6-2020
Date: 7-6-2020
|
The golden angle is the angle that divides a full angle in a golden ratio (but measured in the opposite direction so that it measures less than 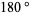 ), i.e.,
), i.e.,
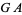 |
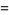 |
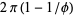 |
(1) |
 |
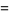 |
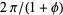 |
(2) |
 |
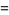 |
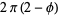 |
(3) |
 |
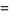 |
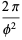 |
(4) |
 |
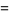 |
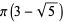 |
(5) |
 |
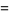 |
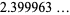 |
(6) |
 |
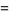 |
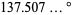 |
(7) |
(OEIS A131988 and A096627; Livio 2002, p. 112).
It is implemented in the Wolfram Language as GoldenAngle.
van Iterson showed in 1907 that points separated by 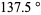 on a tightly bound spiral tends to produce interlocked spirals winding in opposite directions, and that the number of spirals in these two families tend to be consecutive Fibonacci numbers (Livio 2002, p. 112).
on a tightly bound spiral tends to produce interlocked spirals winding in opposite directions, and that the number of spirals in these two families tend to be consecutive Fibonacci numbers (Livio 2002, p. 112).
Another angle related to the golden ratio is the angle
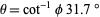 |
(8) |
or twice this angle
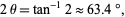 |
(9) |
the later of which is the smaller interior angle in the golden rhombus.
REFERENCES:
Livio, M. The Golden Ratio: The Story of Phi, the World's Most Astonishing Number. New York: Broadway Books, 2002.
Sloane, N. J. A. Sequence A096627 and A131988 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|