Pythagoras's Constant

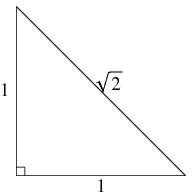
In this work, the name Pythagoras's constant will be given to the square root of 2,

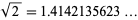(1)

(OEIS A002193), which the Pythagoreans proved to be irrational.

In particular, 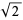 is the length of the hypotenuse of an isosceles right triangle with legs of length one, and the statement that it is irrational means that it cannot be expressed as a ratio  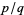of integers  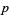and 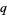. Legend has it that the Pythagorean philosopher Hippasus used geometric methods to demonstrate the irrationality of  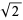while at sea and, upon notifying his comrades of his great discovery, was immediately thrown overboard by the fanatic Pythagoreans. A slight generalization is sometimes known as Pythagoras's theorem.

Theodorus subsequently proved that the square roots of the numbers from 3 to 17 (excluding 4, 9,and 16) are also irrational (Wells 1986, p. 34).

It is not known if Pythagoras's constant is normal to any base (Stoneham 1970, Bailey and Crandall 2003).

The continued fraction for 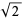 is periodic, as are all quadratic surds,

(2)

(OEIS A040000).

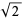 has the Engel expansion 1, 3, 5, 5, 16, 18, 78, 102, 120, ... (OEIS A028254).

It is apparently not known if any BBP-type formula exists for 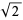, but 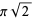 has the formulas

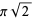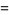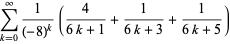			(3)
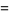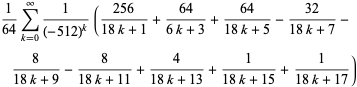			(4)
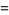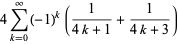			(5)
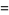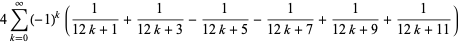			(6)
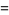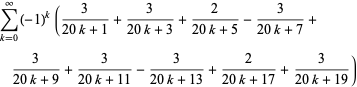			(7)
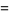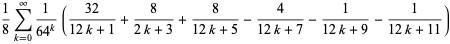			(8)

(E. W. Weisstein, Aug. 30, 2008).

The binary representation for 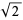 is given by

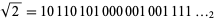(9)

(OEIS A004539; Graham and Polack 1970; Bailey et al. 2003).

Using the Bhaskara-Brouncker square root algorithm for the case 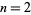, this gives the convergents to  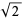as 1, 3/2, 7/5, 17/12, 41/29, 99/70, ... (OEIS A001333 and A000129; Wells 1986, p. 34; Flannery and Flannery 2000, p. 132; Derbyshire 2004, p. 16). The numerators are given by the solutions to the linear recurrence equation

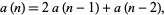(10)

given by

(11)

and the denominators are the Pell numbers, i.e., solutions to the same recurrence equation with 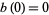 and 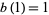, which has solution

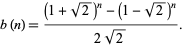(12)

Every other value of 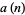, i.e., 1, 7, 41, 239, ... (OEIS A002315) produces the NSW numbers.

Ribenboim (1996, p. 369) considers prime values of 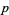 such that  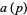is prime, although he mistakenly refers to these as values of  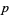that yield prime NSW numbers. The first few such  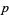are 3, 5, 7, 19, 29, 47, 59, 163, 257, 421, 937, 947, 1493, 1901, ... (OEIS A005850).

For 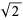, the Newton's iteration square root algorithm gives the convergents 1, 3/2, 17/12, 577/408, 665857/470832, ... (OEIS A001601 and A051009).

The Babylonians gave the impressive approximation

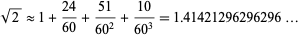(13)

REFERENCES:

Bailey, D. H.; Borwein, J.; Crandall, R. E.; and Pomerance, C. "On the Binary Expansions of Algebraic Numbers." J. Théor. Nombres Bordeaux 16, 487-518, 2004.

Bailey, D. H. and Crandall, R. E. "Random Generators and Normal Numbers." Exper. Math. 11, 527-546, 2002.

Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, p. 25 and 181-182, 1996.

Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.

Finch, S. R. "Pythagoras' Constant." §1.1 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 1-5, 2003.

Flannery, D. The Square Root of 2: A Dialogue Concerning a Number and a Sequence. New York: Copernicus, 2006.

Flannery, S. and Flannery, D. In Code: A Mathematical Journey. London: Profile Books, pp. 130-132, 2000.

Good, I. J. and Gover, T. N. "The Generalized Serial Test and the Binary Expansion of 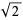." J. Roy. Statist. Soc. Ser. A 130, 102-107, 1967.

Good, I. J. and Gover, T. N. "Corrigendum." J. Roy. Statist. Soc. Ser. A 131, 434, 1968.

Gourdon, X. and Sebah, P. "Pythagore's Constant: 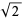." http://numbers.computation.free.fr/Constants/Sqrt2/sqrt2.html.

Graham, R. L. and Pollak, H. O. "Note on a Nonlinear Recurrence Related to 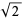." Math. Mag. 43, 143-145, 1970.

Guy, R. K. "Review: The Mathematics of Plato's Academy." Amer. Math. Monthly 97, 440-443, 1990.

Jones, M. F. "22900D [sic] Approximations to the Square Roots of the Primes Less Than 100." Math. Comput. 22, 234-235, 1968.

Nagell, T. Introduction to Number Theory. New York: Wiley, p. 34, 1951.

Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, 1996.

Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, p. 126, 1993.

Sloane, N. J. A. Sequences A000129/M1314, A001333/M2665, A001601/M3042, A002193/M3195, A004539, A005850/M2426, A028254, A040000, A051009, and A070197 in "The On-Line Encyclopedia of Integer Sequences."

Stoneham, R. "A General Arithmetic Construction of Transcendental Non-Liouville Normal Numbers from Rational Functions." Acta Arith. 16, 239-253, 1970.

Uhler, H. S. "Many-Figures Approximations to 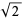, and Distribution of Digits in  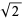and 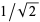." Proc. Nat. Acad. Sci. U.S.A. 37, 63-67, 1951.

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, pp. 34-35, 1986.