


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 4-11-2019
Date: 30-12-2019
Date: 6-1-2020
|
Successive application of Archimedes' recurrence formula gives the Archimedes algorithm, which can be used to provide successive approximations to 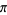 (pi). The algorithm is also called the Borchardt-Pfaff algorithm. Archimedes obtained the first rigorous approximation of
(pi). The algorithm is also called the Borchardt-Pfaff algorithm. Archimedes obtained the first rigorous approximation of 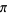 by circumscribing and inscribing
by circumscribing and inscribing 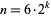 -gons on a circle. From Archimedes' recurrence formula, the circumferences
-gons on a circle. From Archimedes' recurrence formula, the circumferences 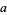 and
and 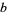 of the circumscribed and inscribed polygons are
of the circumscribed and inscribed polygons are
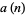 |
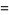 |
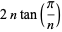 |
(1) |
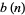 |
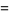 |
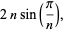 |
(2) |
where
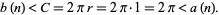 |
(3) |
For a hexagon, 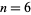 and
and
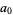 |
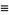 |
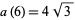 |
(4) |
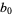 |
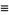 |
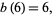 |
(5) |
where 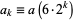 . The first iteration of Archimedes' recurrence formula then gives
. The first iteration of Archimedes' recurrence formula then gives
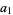 |
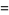 |
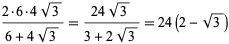 |
(6) |
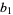 |
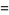 |
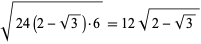 |
(7) |
 |
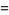 |
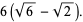 |
(8) |
Additional iterations do not have simple closed forms, but the numerical approximations for 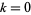 , 1, 2, 3, 4 (corresponding to 6-, 12-, 24-, 48-, and 96-gons) are
, 1, 2, 3, 4 (corresponding to 6-, 12-, 24-, 48-, and 96-gons) are
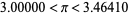 |
(9) |
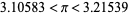 |
(10) |
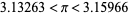 |
(11) |
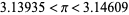 |
(12) |
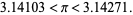 |
(13) |
By taking 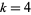 (a 96-gon) and using strict inequalities to convert irrational bounds to rational bounds at each step, Archimedes obtained the slightly looser result
(a 96-gon) and using strict inequalities to convert irrational bounds to rational bounds at each step, Archimedes obtained the slightly looser result
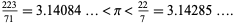 |
(14) |
REFERENCES:
Miel, G. "Of Calculations Past and Present: The Archimedean Algorithm." Amer. Math. Monthly 90, 17-35, 1983.
Phillips, G. M. "Archimedes in the Complex Plane." Amer. Math. Monthly 91, 108-114, 1984.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|