Repeating Decimal

A repeating decimal, also called a recurring decimal, is a number whose decimal representation eventually becomes periodic (i.e., the same sequence of digits repeats indefinitely). The repeating portion of a decimal expansion is conventionally denoted with a vinculum so, for example,

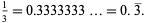The minimum number of digits that repeats in such a number is known as the decimal period.

Repeating decimal notation was implemented in versions of the Wolfram Language prior to 6 as PeriodicForm[RealDigits[r]] after loading the add-on package NumberTheory`ContinuedFractions`.

All rational numbers have either finite decimal expansions (i.e., are regular numbers; e.g., 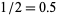) or repeating decimals (e.g., 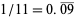). However, irrational numbers, such as  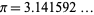neither terminate nor become periodic.

Numbers such as 0.5 are sometimes regarded as repeating decimals since .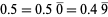

The denominators of the first few unit fractions having repeating decimals are 3, 6, 7, 9, 11, 12, 13, 14, 15, 17, 18, 19, 21, 22, 23, 24, 26, 27, 28, 29, ... (OEIS A085837).

The repeating portion of a rational number can be found in the Wolfram Language using the command RealDigits[r][[1,-1]]. The number of digits in the repeating portion of the decimal expansion of a rational number can also be found directly from the multiplicative order of its denominator. The periods of the decimal expansions of 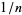 for 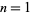, 2, ... are 0, 0, 1, 0, 0, 1, 6, 0, 1, 0, 2, 1, 6, 6, 1, 0, 16, 1, 18, ... (OEIS A051626), where 0 indicates that the number is regular.

If 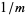 is a repeating decimal and  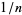is a terminating decimal, them  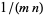has a nonperiodic part whose length is that of  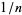and a repeating part whose length is that of  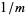(Wells 1986, p. 60).

REFERENCES:

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 53-54, 1987.

Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 167-168, 1996.

Courant, R. and Robbins, H. "Rational Numbers and Periodic Decimals." §2.2.4 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 66-68, 1996.

Sloane, N. J. A. Sequences A051626 and A085837 in "The On-Line Encyclopedia of Integer Sequences."

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 60, 1986.