


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 15-11-2020
Date: 22-10-2019
Date: 9-1-2021
|
For a real number 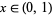 , let
, let 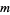 be the number of terms in the convergent to a regular continued fraction that are required to represent
be the number of terms in the convergent to a regular continued fraction that are required to represent 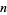 decimal places of
decimal places of  . Then Lochs' theorem states that for almost all
. Then Lochs' theorem states that for almost all  ,
,
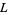 |
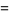 |
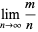 |
(1) |
 |
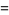 |
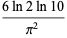 |
(2) |
 |
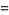 |
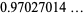 |
(3) |
(OEIS A086819; Lochs 1964). This number is sometimes known as Lochs' constant.
The reciprocal of this constant is
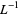 |
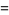 |
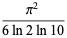 |
(4) |
 |
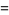 |
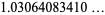 |
(5) |
(OEIS A062542; Finch 2003, p. 60).
Lochs' constant is related to the Lévy constant 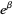 by
by
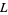 |
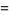 |
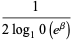 |
(6) |
 |
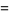 |
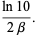 |
(7) |
In the index and table of constants Finch (2003, pp. 546 and 596) refers to the quantity
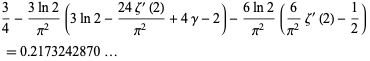 |
(8) |
related to Porter's constant as "Lochs' constant," though this terminology appears to be nonstandard.
REFERENCES:
Bosma, W.; Dajani, K.; and Kraaikamp, C. "Entropy and Counting Correct Digits." Univ. Nijmegen Math. Report 9925, 1999.
Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, 2003.
Kintchine, A. "Zur metrischen Kettenbruchtheorie." Compos. Math. 3, 276-285, 1936.
Kraaikamp, C. "A New Class of Continued Fraction Expansions." Acta Arith. 57, 1-39, 1991.
Lévy, P. "Sur le developpement en fraction continue d'un nombre choisi au hasard." Compos. Math. 3, 286-303, 1936.
Lochs, G. "Vergleich der Genauigkeit von Dezimalbruch und Kettenbruch." Abh. Hamburg Univ. Math. Sem. 27, 142-144, 1964.
Perron, O. Die Lehre von den Kettenbrüchen, 3. verb. und erweiterte Aufl. Stuttgart, Germany: Teubner, 1954-57.
Sloane, N. J. A. Sequences A062542 and A086819 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|