


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 29-8-2020
Date: 4-11-2019
Date: 5-1-2020
|
A fractional ideal is a generalization of an ideal in a ring 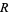 . Instead, a fractional ideal is contained in the number field
. Instead, a fractional ideal is contained in the number field 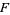 , but has the property that there is an element
, but has the property that there is an element 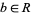 such that
such that
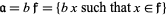 |
(1) |
is an ideal in 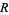 . In particular, every element in
. In particular, every element in 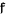 can be written as a fraction, with a fixed denominator.
can be written as a fraction, with a fixed denominator.
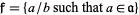 |
(2) |
Note that the multiplication of two fractional ideals is another fractional ideal.
For example, in the field 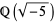 , the set
, the set
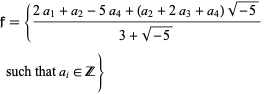 |
(3) |
is a fractional ideal because
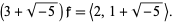 |
(4) |
Note that 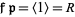 , where
, where
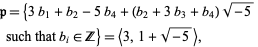 |
(5) |
and so 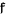 is an inverse to
is an inverse to 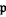 .
.
Given any fractional ideal 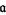 there is always a fractional ideal
there is always a fractional ideal 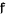 such that
such that 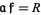 . Consequently, the fractional ideals form an Abelian group by multiplication. The principal ideals generate a subgroup
. Consequently, the fractional ideals form an Abelian group by multiplication. The principal ideals generate a subgroup 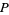 , and the quotient group is called the ideal class group.
, and the quotient group is called the ideal class group.
REFERENCES:
Atiyah, M. and MacDonald, I. Ch. 9 in Introduction to Commutative Algebra. Reading, MA: Addison-Wesley, 1969.
Cohn, H. Introduction to the Construction of Class Fields. New York: Cambridge University Press, p. 32, 1985.
Fröhlich, A. and Taylor, M. Ch. 2 in Algebraic Number Theory. New York: Cambridge University Press, 1991.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|