


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-8-2018
Date: 30-3-2019
Date: 18-8-2018
|
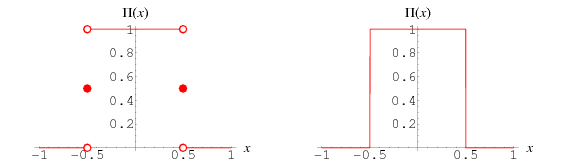
The rectangle function  is a function that is 0 outside the interval
is a function that is 0 outside the interval ![[-1/2,1/2]](http://mathworld.wolfram.com/images/equations/RectangleFunction/Inline2.gif) and unity inside it. It is also called the gate function, pulse function, or window function, and is defined by
and unity inside it. It is also called the gate function, pulse function, or window function, and is defined by
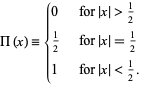 |
(1) |
The left figure above plots the function as defined, while the right figure shows how it would appear if traced on an oscilloscope. The generalized function 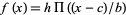 has height
has height 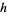 , center
, center 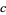 , and full-width
, and full-width 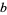 .
.
As noted by Bracewell (1965, p. 53), "It is almost never important to specify the values at 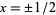 , that is at the points of discontinuity. Likewise, it is not necessary or desirable to emphasize the values
, that is at the points of discontinuity. Likewise, it is not necessary or desirable to emphasize the values 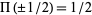 in graphs; it is preferable to show graphs which are reminiscent of high-quality oscillograms (which, of course, would never show extra brightening halfway up the discontinuity)."
in graphs; it is preferable to show graphs which are reminiscent of high-quality oscillograms (which, of course, would never show extra brightening halfway up the discontinuity)."
The piecewise version of the rectangle function is implemented in the Wolfram Language as UnitBox[x], while the generalized function version is implemented as HeavisidePi[x].
Identities satisfied by the rectangle function include
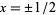 |
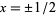 |
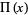 |
(2) |
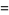 |
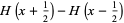 |
 |
(3) |
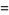 |
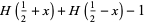 |
 |
(4) |
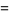 |
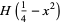 |
![1/2[sgn(x+1/2)-sgn(x-1/2)],](http://mathworld.wolfram.com/images/equations/RectangleFunction/Inline20.gif) |
(5) |
where 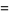 is the Heaviside step function. The Fourier transform of the rectangle function is given by
is the Heaviside step function. The Fourier transform of the rectangle function is given by
](http://mathworld.wolfram.com/images/equations/RectangleFunction/Inline22.gif) |
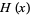 |
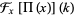 |
(6) |
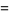 |
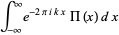 |
 |
(7) |
where 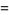 is the sinc function.
is the sinc function.
REFERENCES:
Bracewell, R. "Rectangle Function of Unit Height and Base, 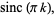 ." In The Fourier Transform and Its Applications. New York: McGraw-Hill, pp. 52-53, 1965.
." In The Fourier Transform and Its Applications. New York: McGraw-Hill, pp. 52-53, 1965.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|