المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Meixner Polynomial of the Second Kind |
 1267
 03:55 مساءً
date: 20-9-2019 |
Author : Chihara, T. S. 
Book or Source : An Introduction to Orthogonal Polynomials. New York: Gordon and Breach 
Page and Part : ...|
Read More
Date: 23-5-2019
2183
Date: 21-5-2019
1569
Date: 28-4-2019
2199
|
The polynomials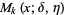 
which form the Sheffer sequence for
 |
 |
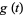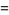![{[1+deltaf(t)]^2+[f(t)]^2}^(eta/2)](http://mathworld.wolfram.com/images/equations/MeixnerPolynomialoftheSecondKind/Inline4.gif) |
(1) |
 |
 |
 |
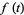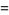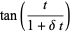(2) |
which have generating function
![sum_(k=0)^infty(M_k(x;delta,eta))/(k!)t^k
=[(1+deltat)^2]^(-eta/2)exp((xtan^(-1)t)/(1-deltatan^(-1)t)).](http://mathworld.wolfram.com/images/equations/MeixnerPolynomialoftheSecondKind/NumberedEquation1.gif) |
(3) |
The first few are
 |
 |
 |
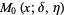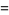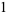(4) |
 |
 |
 |
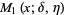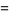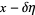(5) |
 |
 |
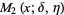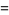![x^2+2delta(1-eta)x+eta[(eta+1)delta^2-1].](http://mathworld.wolfram.com/images/equations/MeixnerPolynomialoftheSecondKind/Inline16.gif) |
(6) |
REFERENCES:
Chihara, T. S. An Introduction to Orthogonal Polynomials. New York: Gordon and Breach, p. 179, 1978.
Roman, S. The Umbral Calculus. New York: Academic Press, 1984.
|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|
