Binet,s Log Gamma Formulas
المؤلف:
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G.
المصدر:
Higher Transcendental Functions, Vol. 1. New York: Krieger, 1981.
الجزء والصفحة:
...
21-5-2019
1994
Binet's Log Gamma Formulas
Binet's first formula for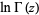 
, where 
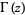is a gamma function, is given by
for ![R[z]>0](http://mathworld.wolfram.com/images/equations/BinetsLogGammaFormulas/Inline3.gif)
(Erdélyi et al. 1981, p. 21; Whittaker and Watson 1990, p. 249).
Binet's second formula is
for ![R[z]>0](http://mathworld.wolfram.com/images/equations/BinetsLogGammaFormulas/Inline4.gif)
(Erdélyi et al. 1981, p. 22; Whittaker and Watson 1990, pp. 250-251).
REFERENCES:
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. Higher Transcendental Functions, Vol. 1. New York: Krieger, 1981.
Whittaker, E. T. and Watson, G. N. "Binet's First Expansion for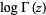 
in Terms of an Infinite Integral" and "Binet's Second Expression for 
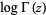in Terms of an Infinite Integral." §12.31 and 12.32 in A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, pp. 248-251, 1990.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
