المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Mahler Polynomial |
 1052
 05:26 مساءً
date: 19-9-2019 |
Author : Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. 
Book or Source : Higher Transcendental Functions, Vol. 3. New York: Krieger 
Page and Part : ...|
Read More
Date: 9-10-2019
1472
Date: 16-5-2018
1816
Date: 24-9-2018
1822
|
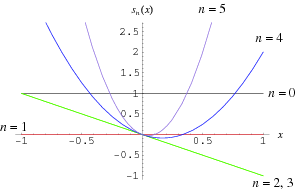
Polynomials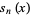 
which form the Sheffer sequence for
 |
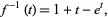(1) |
where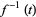 
is the inverse function of 
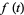, and have generating function
 |
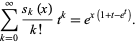(2) |
The first few are
 |
 |
 |
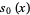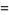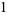(3) |
 |
 |
 |
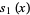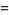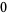(4) |
 |
 |
 |
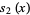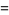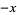(5) |
 |
 |
 |
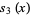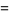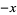(6) |
 |
 |
 |
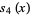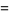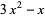(7) |
 |
 |
 |
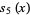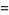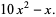(8) |
REFERENCES:
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. Higher Transcendental Functions, Vol. 3. New York: Krieger, p. 254, 1981.
Roman, S. The Umbral Calculus. New York: Academic Press, 1984.
|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|
