المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | G-Function |
 1555
 06:02 مساءً
date: 8-8-2019 |
Author : Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G 
Book or Source : The Function G(z)." §1.8 in Higher Transcendental Functions, Vol. 1. New York: Krieger, 
Page and Part : pp. 20 and 44-46|
Read More
Date: 25-3-2019
1545
Date: 25-3-2019
2087
Date: 13-9-2019
3430
|
 |
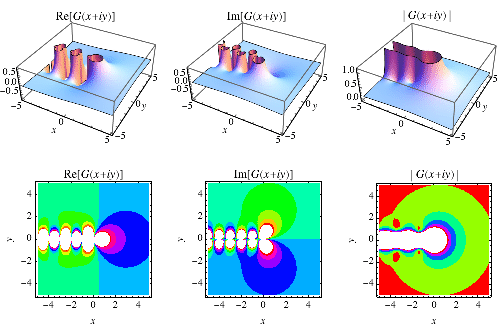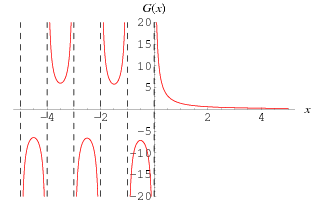
As defined by Erdélyi et al. (1981, p. 20), the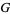 
-function is given by
 |
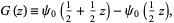(1) |
where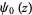 
is the digamma function. Integral representations are given by
 |
 |
 |
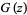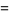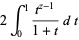(2) |
 |
 |
 |
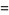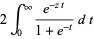(3) |
for ![R[z]>0](http://mathworld.wolfram.com/images/equations/G-Function/Inline9.gif)
. 
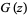is also given by the series
 |
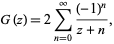(4) |
and in terms of the hypergeometric function by
 |
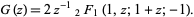(5) |
It obeys the functional relations
 |
 |
 |
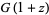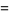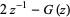(6) |
 |
 |
 |
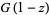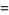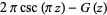(7) |
 |
 |
 |
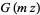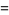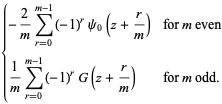(8) |
REFERENCES:
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. "The Function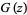 
." §1.8 in Higher Transcendental Functions, Vol. 1. New York: Krieger, pp. 20 and 44-46, 1981.
|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
أصواتٌ قرآنية واعدة .. أكثر من 80 برعماً يشارك في المحفل القرآني الرمضاني بالصحن الحيدري الشريف
|
|
|
