


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-8-2019
Date: 21-9-2018
Date: 25-7-2019
|
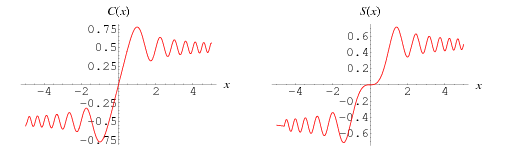
There are a number of slightly different definitions of the Fresnel integrals. In physics, the Fresnel integrals denoted 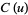 and
and 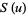 are most often defined by
are most often defined by
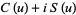 |
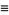 |
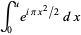 |
(1) |
 |
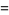 |
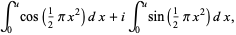 |
(2) |
so
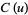 |
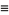 |
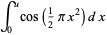 |
(3) |
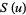 |
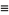 |
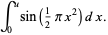 |
(4) |
These Fresnel integrals are implemented in the Wolfram Language as FresnelC[z] and FresnelS[z].
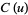 and
and 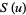 are entire functions.
are entire functions.
 |
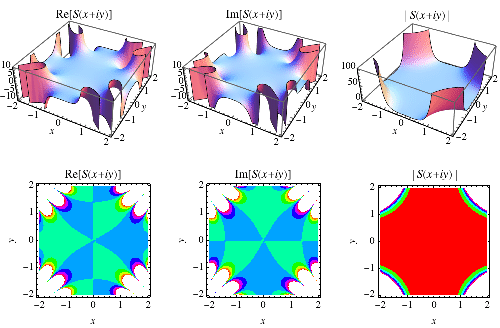 |
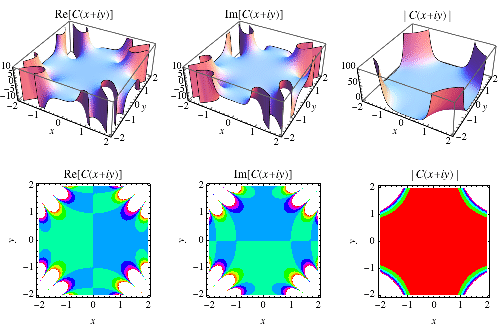
The 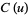 and
and 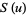 integrals are illustrated above in the complex plane.
integrals are illustrated above in the complex plane.
They have the special values
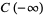 |
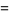 |
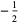 |
(5) |
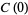 |
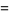 |
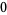 |
(6) |
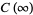 |
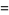 |
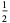 |
(7) |
and
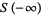 |
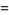 |
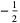 |
(8) |
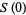 |
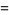 |
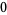 |
(9) |
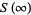 |
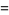 |
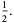 |
(10) |
An asymptotic expansion for 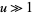 gives
gives
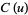 |
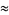 |
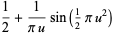 |
(11) |
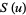 |
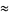 |
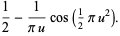 |
(12) |
Therefore, as 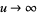 ,
, 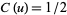 and
and 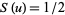 . The Fresnel integrals are sometimes alternatively defined as
. The Fresnel integrals are sometimes alternatively defined as
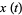 |
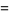 |
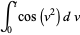 |
(13) |
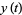 |
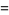 |
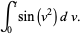 |
(14) |
Letting 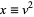 so
so 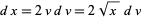 , and
, and 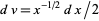
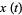 |
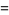 |
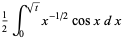 |
(15) |
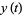 |
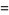 |
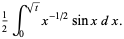 |
(16) |
In this form, they have a particularly simple expansion in terms of spherical Bessel functions of the first kind. Using
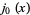 |
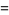 |
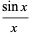 |
(17) |
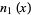 |
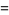 |
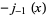 |
(18) |
 |
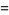 |
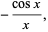 |
(19) |
where 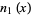 is a spherical Bessel function of the second kind
is a spherical Bessel function of the second kind
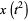 |
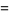 |
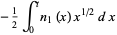 |
(20) |
 |
 |
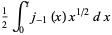 |
(21) |
 |
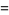 |
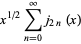 |
(22) |
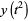 |
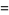 |
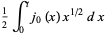 |
(23) |
 |
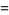 |
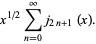 |
(24) |
Related functions 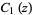 ,
, 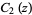 ,
, 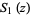 , and
, and 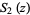 are defined by
are defined by
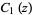 |
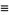 |
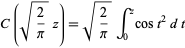 |
(25) |
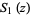 |
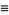 |
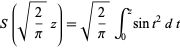 |
(26) |
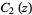 |
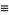 |
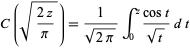 |
(27) |
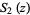 |
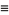 |
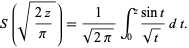 |
(28) |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Fresnel Integrals." §7.3 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 300-302, 1972.
Leonard, I. E. "More on Fresnel Integrals." Amer. Math. Monthly 95, 431-433, 1988.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Fresnel Integrals, Cosine and Sine Integrals." §6.79 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 248-252, 1992.
Prudnikov, A. P.; Marichev, O. I.; and Brychkov, Yu. A. "The Generalized Fresnel Integrals 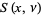 and
and 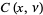 ." §1.3 in Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach, p. 24, 1990.
." §1.3 in Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach, p. 24, 1990.
Spanier, J. and Oldham, K. B. "The Fresnel Integrals 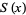 and
and 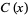 ." Ch. 39 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 373-383, 1987.
." Ch. 39 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 373-383, 1987.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|