


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-9-2018
Date: 20-8-2018
Date: 22-5-2019
|
A q-analog of the gamma function defined by
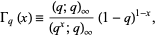 |
(1) |
where 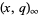 is a q-Pochhammer symbol (Koepf 1998, p. 26; Koekoek and Swarttouw 1998). The
is a q-Pochhammer symbol (Koepf 1998, p. 26; Koekoek and Swarttouw 1998). The 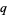 -gamma function satisfies
-gamma function satisfies
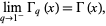 |
(2) |
where 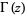 is the gamma function (Andrews 1986).
is the gamma function (Andrews 1986).
The 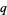 -gamma function is implemented in the Wolfram Language as QGamma[z, q].
-gamma function is implemented in the Wolfram Language as QGamma[z, q].
The 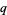 -gamma function satisfies the functional equation
-gamma function satisfies the functional equation
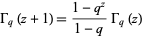 |
(3) |
with 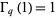 (Koekoek and Swarttouw 1998, p. 10), which simplifies to
(Koekoek and Swarttouw 1998, p. 10), which simplifies to
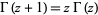 |
(4) |
as 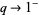 . A curious identity for the functional equation
. A curious identity for the functional equation
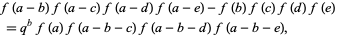 |
(5) |
where
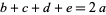 |
(6) |
is given by
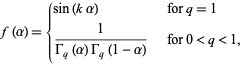 |
(7) |
for any 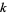 .
.
REFERENCES:
Andrews, G. E. "W. Gosper's Proof that 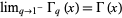 ." Appendix A in q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math. Soc., p. 11 and 109, 1986.
." Appendix A in q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math. Soc., p. 11 and 109, 1986.
Gasper, G. and Rahman, M. Basic Hypergeometric Series. Cambridge, England: Cambridge University Press, 1990.
Koekoek, R. and Swarttouw, R. F. "The q-Gamma Function and the q-Binomial Coefficient." §0.3 in The Askey-Scheme of Hypergeometric Orthogonal Polynomials and its q-Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, pp. 10-11, 1998.
Koepf, W. Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, 1998.
Wenchang, C. Problem 10226 and Solution. "A q-Trigonometric Identity." Amer. Math. Monthly 103, 175-177, 1996.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|