المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Whipple,s Transformation |
 1320
 06:07 مساءً
date: 20-6-2019 |
Author : Andrews, G. E. and Burge, W. H. 
Book or Source : "Determinant Identities." Pacific J. Math. 158 
Page and Part : ...|
Read More
Date: 21-9-2019
1664
Date: 25-4-2019
1850
Date: 29-8-2019
2068
|
![_7F_6[a,1+1/2a,b,c,d,e,-m; 1/2a,1+a-b,1+a-c, ; 1+a-d,1+a-e,1+a+m]
=((1+a)_m(1+a-d-e)_m)/((1+a-d)_m(1+a-e)_m)_4F_3[1+a-b-c,d,e,-m; 1+a-b,1+a-c,d+e-a-m]](http://mathworld.wolfram.com/images/equations/WhipplesTransformation/NumberedEquation1.gif) |
(Bailey 1935, p. 25), where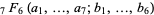 
and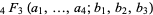 
are generalized hypergeometric functions with argument 
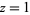and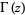 
is the gamma function.
Another transformation due to Whipple (1926ab) is given by
![_4F_3[a,b,-z,-n; u,v,w;1]
=(Gamma(u+z+n)Gamma(w+z+n)Gamma(v)Gamma(w))/(Gamma(v+z)Gamma(v+n)Gamma(w+n)Gamma(w+z))_4F_3[u-a,u-b,-z,-n; 1-v-z-n,1-w-z-n,u;1]](http://mathworld.wolfram.com/images/equations/WhipplesTransformation/NumberedEquation2.gif) |
for one of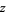 
and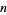 
a nonnegative integer (Andrews and Burge 1993).
REFERENCES:
Andrews, G. E. and Burge, W. H. "Determinant Identities." Pacific J. Math. 158, 1-14, 1993.
Bailey, W. N. Generalised Hypergeometric Series. Cambridge, England: Cambridge University Press, pp. 25 and 29, 1935.
Whipple, F. J. W. "On Well-Poised Series, Generalized Hypergeometric Series Having Parameters in Pairs, Each Pair with the Same Sum." Proc. London Math. Soc. 24, 247-263, 1926a.
Whipple, F. J. W. "Well-Poised Series and Other Generalized Hypergeometric Series." Proc. London Math. Soc. Ser. 2 25, 525-544, 1926b.
Whipple, F. J. W. "A Fundamental Relation Between Generalized Hypergeometric Series." Proc. London Math. Soc. 26, 257-272, 1927.
|
|
|
|
دور في الحماية من السرطان.. يجب تناول لبن الزبادي يوميا
|
|
|
|
|
|
|
العلماء الروس يطورون مسيرة لمراقبة حرائق الغابات
|
|
|
|
|
|
|
ضمن أسبوع الإرشاد النفسي.. جامعة العميد تُقيم أنشطةً ثقافية وتطويرية لطلبتها
|
|
|
