


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-10-2018
Date: 26-7-2019
Date: 23-4-2019
|
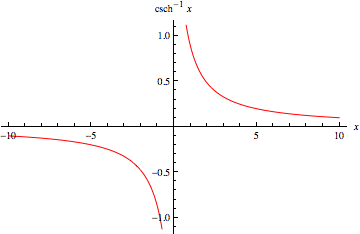 |
 |
The inverse hyperbolic cosecant 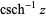 (Zwillinger 1995, p. 481), sometimes called the area hyperbolic cosecant (Harris and Stocker 1998, p. 271) and sometimes denoted
(Zwillinger 1995, p. 481), sometimes called the area hyperbolic cosecant (Harris and Stocker 1998, p. 271) and sometimes denoted 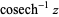 (Beyer 1987, p. 181) or
(Beyer 1987, p. 181) or 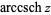 (Abramowitz and Stegun 1972, p. 87; Jeffrey 2000, p. 124), is the multivalued function that is the inverse function of the hyperbolic cosecant. The variants
(Abramowitz and Stegun 1972, p. 87; Jeffrey 2000, p. 124), is the multivalued function that is the inverse function of the hyperbolic cosecant. The variants 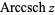 (Abramowitz and Stegun 1972, p. 87) and
(Abramowitz and Stegun 1972, p. 87) and 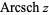 (Harris and Stocker 1998, p. 263) are sometimes used to refer to explicit principal values. Worse yet, the notation
(Harris and Stocker 1998, p. 263) are sometimes used to refer to explicit principal values. Worse yet, the notation 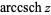 is sometimes used for the principal value, with
is sometimes used for the principal value, with 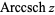 being used for the multivalued function (Abramowitz and Stegun 1972, p. 87). Note that in the notation
being used for the multivalued function (Abramowitz and Stegun 1972, p. 87). Note that in the notation 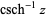 ,
, 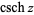 is the hyperbolic cosecant and the superscript
is the hyperbolic cosecant and the superscript 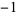 denotes an inverse function, not the multiplicative inverse.
denotes an inverse function, not the multiplicative inverse.
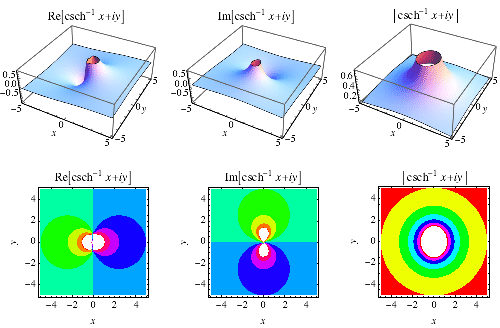
The inverse hyperbolic cosecant is a multivalued function and hence requires a branch cut in the complex plane, which the Wolfram Language's convention places at 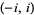 .
.
The principal value of 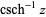 is implemented in the Wolfram Language as ArcCsch[z].
is implemented in the Wolfram Language as ArcCsch[z].
It has special value
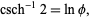 |
(1) |
where 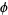 is the golden ratio.
is the golden ratio.

The inverse hyperbolic cosecant is a multivalued function and hence requires a branch cut in the complex plane, which the Wolfram Language's convention places at the line segment 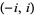 . This follows from the definition of
. This follows from the definition of 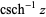 as
as
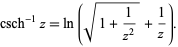 |
(2) |
The derivative of the inverse hyperbolic cosecant is
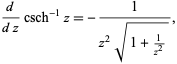 |
(3) |
and the indefinite integral is
![intcsch^(-1)zdz
=zcsch^(-1)z+ln[z(1+sqrt((1+z^2)/(z^2)))]+C.](http://mathworld.wolfram.com/images/equations/InverseHyperbolicCosecant/NumberedEquation4.gif) |
(4) |
For real  , it satisfies
, it satisfies
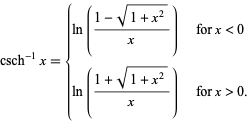 |
(5) |
The inverse hyperbolic cosecant has Puiseux series
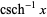 |
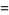 |
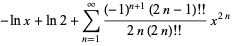 |
(6) |
 |
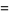 |
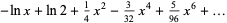 |
(7) |
(OEIS A052468 and A052469) about 0, and Taylor series about 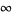 of
of
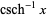 |
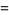 |
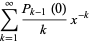 |
(8) |
 |
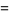 |
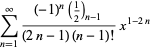 |
(9) |
 |
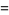 |
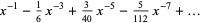 |
(10) |
(OEIS A055786 and A002595), where 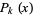 is a Legendre polynomial and
is a Legendre polynomial and 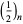 is a Pochhammer symbol.
is a Pochhammer symbol.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Inverse Hyperbolic Functions." §4.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 86-89, 1972.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 142-143, 1987.
Harris, J. W. and Stocker, H. Handbook of Mathematics and Computational Science. New York: Springer-Verlag, 1998.
Jeffrey, A. "Inverse Trigonometric and Hyperbolic Functions." §2.7 in Handbook of Mathematical Formulas and Integrals, 2nd ed.Orlando, FL: Academic Press, pp. 124-128, 2000.
Sloane, N. J. A. Sequences A052468, A052469, A055786 and A002595/M4233 in "The On-Line Encyclopedia of Integer Sequences."
Spanier, J. and Oldham, K. B. "Inverse Trigonometric Functions." Ch. 35 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 331-341, 1987.
Zwillinger, D. (Ed.). "Inverse Hyperbolic Functions." §6.8 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 481-483, 1995.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|