


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 31-7-2019
Date: 30-9-2019
Date: 14-10-2019
|
The Wigner 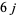 -symbols (Messiah 1962, p. 1062), commonly simply called the
-symbols (Messiah 1962, p. 1062), commonly simply called the 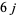 -symbols, are a generalization of Clebsch-Gordan coefficients and Wigner 3j-symbol that arise in the coupling of three angular momenta. They are variously called the "
-symbols, are a generalization of Clebsch-Gordan coefficients and Wigner 3j-symbol that arise in the coupling of three angular momenta. They are variously called the "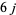 symbols" (Messiah 1962, p. 1062) or 6-
symbols" (Messiah 1962, p. 1062) or 6-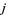 symbols (Shore and Menzel 1968, p. 279).
symbols (Shore and Menzel 1968, p. 279).
The Wigner 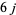 -symbols are returned by the Wolfram Language function SixJSymbol[
-symbols are returned by the Wolfram Language function SixJSymbol[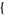 j1, j2, j3
j1, j2, j3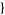 ,
, 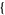 j4, j5, j6
j4, j5, j6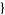 ].
].
Let tensor operators 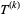 and
and 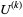 act, respectively, on subsystems 1 and 2 of a system, with subsystem 1 characterized by angular momentum
act, respectively, on subsystems 1 and 2 of a system, with subsystem 1 characterized by angular momentum 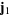 and subsystem 2 by the angular momentum
and subsystem 2 by the angular momentum 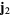 . Then the matrix elements of the scalar product of these two tensor operators in the coupled basis
. Then the matrix elements of the scalar product of these two tensor operators in the coupled basis 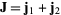 are given by
are given by
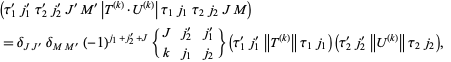 |
(1) |
where 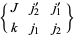 is the Wigner
is the Wigner 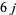 -symbol and
-symbol and 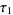 and
and 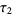 represent additional pertinent quantum numbers characterizing subsystems 1 and 2 (Gordy and Cook 1984).
represent additional pertinent quantum numbers characterizing subsystems 1 and 2 (Gordy and Cook 1984).
The 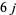 symbols are denoted
symbols are denoted 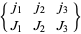 and are defined for integers and half-integers
and are defined for integers and half-integers 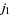 ,
, 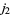 ,
, 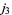 ,
, 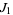 ,
, 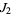 ,
, 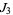 whose triads
whose triads 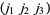 ,
, 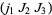 ,
, 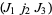 , and
, and 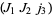 satisfy the following conditions (Messiah 1962, p. 1063).
satisfy the following conditions (Messiah 1962, p. 1063).
1. Each triad satisfies the triangular inequalities.
2. The sum of the elements of each triad is an integer. Therefore, the members of each triad are either all integers or contain two half-integers and one integer.
If these conditions are not satisfied, 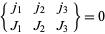 .
.
The 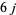 -symbols are invariant under permutation of their columns, e.g.,
-symbols are invariant under permutation of their columns, e.g.,
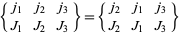 |
(2) |
and under exchange of two corresponding elements between rows, e.g.,
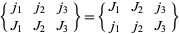 |
(3) |
(Messiah 1962, pp. 1063-1064).
The 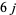 -symbols can be computed using the Racah formula
-symbols can be computed using the Racah formula
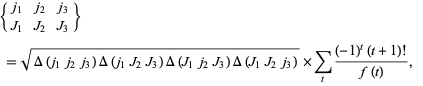 |
(4) |
where 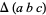 is a triangle coefficient,
is a triangle coefficient,
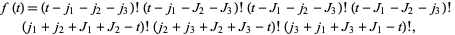 |
(5) |
and the sum is over all integers 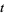 for which the factorials in
for which the factorials in 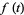 all have nonnegative arguments (Wigner 1959; Messiah 1962, p. 1065; Shore and Menzel 1968, p. 279). In particular, the number of terms is equal to
all have nonnegative arguments (Wigner 1959; Messiah 1962, p. 1065; Shore and Menzel 1968, p. 279). In particular, the number of terms is equal to 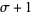 , where
, where 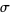 is the smallest of the twelve numbers
is the smallest of the twelve numbers
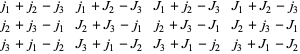 |
(6) |
(Messiah 1962, p. 1064).
The 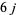 symbols satisfy the so-called Racah-Elliot and orthogonality relations,
symbols satisfy the so-called Racah-Elliot and orthogonality relations,
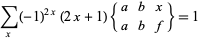 |
(7) |
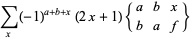 |
(8) |
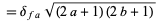 |
(9) |
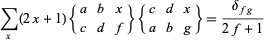 |
(10) |
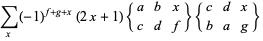 |
(11) |
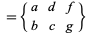 |
(12) |
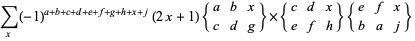 |
(13) |
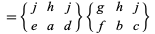 |
(14) |
(Messiah 1962, p. 1065).
Edmonds (1968) gives analytic forms of the 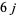 -symbol for simple cases, and Shore and Menzel (1968) and Gordy and Cook (1984) give
-symbol for simple cases, and Shore and Menzel (1968) and Gordy and Cook (1984) give
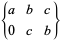 |
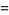 |
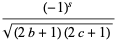 |
(15) |
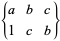 |
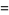 |
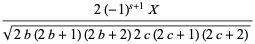 |
(16) |
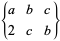 |
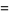 |
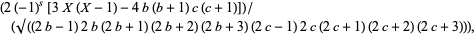 |
(17) |
where
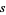 |
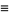 |
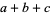 |
(18) |
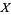 |
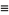 |
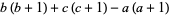 |
(19) |
(Edmonds 1968; Shore and Menzel 1968, p. 281; Gordy and Cook 1984, p. 809). Note that since 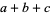 must be an integer,
must be an integer, 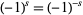 , so replacing the definition of
, so replacing the definition of 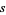 with its negative above gives an equivalent result.
with its negative above gives an equivalent result.
Messiah (1962, p. 1066) gives the additional special cases
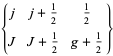 |
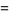 |
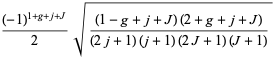 |
(20) |
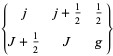 |
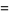 |
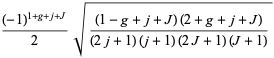 |
(21) |
for 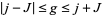 .
.
The Wigner 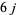 -symbols are related to the Racah W-coefficients by
-symbols are related to the Racah W-coefficients by
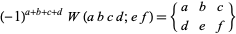 |
(22) |
(Messiah 1962, p. 1062; Shore and Menzel 1968, p. 279).
REFERENCES:
Biedenharn, L. C. and Louck, J. D. The Racah-Wigner Algebra in Quantum Theory. Reading, MA: Addison-Wesley, 1981.
Biedenharn, L. C. and Louck, J. D. Angular Momentum in Quantum Physics: Theory and Applications. Reading, MA: Addison-Wesley, 1981.
Carter, J. S.; Flath, D. E.; and Saito, M. The Classical and Quantum 6j-Symbols. Princeton, NJ: Princeton University Press, 1995.
Edmonds, A. R. Angular Momentum in Quantum Mechanics, 2nd ed., rev. printing. Princeton, NJ: Princeton University Press, 1968.
Gordy, W. and Cook, R. L. Microwave Molecular Spectra, 3rd ed. New York: Wiley, pp. 807-809, 1984.
Messiah, A. "Racah Coefficients and '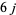 ' Symbols." Appendix C.II in Quantum Mechanics, Vol. 2. Amsterdam, Netherlands: North-Holland, pp. 567-569 and 1061-1066, 1962.
' Symbols." Appendix C.II in Quantum Mechanics, Vol. 2. Amsterdam, Netherlands: North-Holland, pp. 567-569 and 1061-1066, 1962.
Racah, G. "Theory of Complex Spectra. II." Phys. Rev. 62, 438-462, 1942.
Rotenberg, M.; Bivens, R.; Metropolis, N.; and Wooten, J. K. The 3j and 6j Symbols. Cambridge, MA: MIT Press, 1959.
Shore, B. W. and Menzel, D. H. Principles of Atomic Spectra. New York: Wiley, pp. 279-284, 1968.
Wigner, E. P. Group Theory and Its Application to the Quantum Mechanics of Atomic Spectra, expanded and improved ed. New York: Academic Press, 1959.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|