المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Ber |
 1565
 02:03 مساءً
date: 24-3-2019 |
Author : Abramowitz, M. and Stegun, I. A 
Book or Source : "Kelvin Functions." §9.9 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover 
Page and Part : ...|
Read More
Date: 19-9-2018
2010
Date: 19-9-2018
2989
Date: 25-7-2019
1638
|
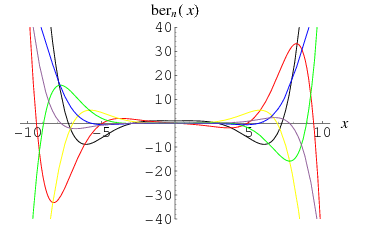
The function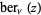 
is defined through the equation
 |
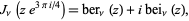(1) |
where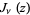 
is a Bessel function of the first kind, so
![ber_nu(z)=R[J_nu(ze^(3pii/4))],](http://mathworld.wolfram.com/images/equations/Ber/NumberedEquation2.gif) |
(2) |
where ![R[z]](http://mathworld.wolfram.com/images/equations/Ber/Inline3.gif)
is the real part.
The function is implemented in the Wolfram Language as KelvinBer[nu, z].
The function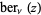 
has the series expansion
![ber_nu(z)=(1/2z)^nusum_(k=0)^infty(cos[(3/4nu+1/2k)pi])/(k!Gamma(nu+k+1))(1/4z^2)^k,](http://mathworld.wolfram.com/images/equations/Ber/NumberedEquation3.gif) |
(3) |
where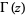 
is the gamma function (Abramowitz and Stegun 1972, p. 379), which can be written in closed form as
![ber_nu(z)=1/2e^(-3ipinu/4)z^nu[(-1)^(1/4)z]^(-nu)
×[e^(3piinu/2)I_nu((-1)^(1/4)z)+J_nu((-1)^(1/4)z)],](http://mathworld.wolfram.com/images/equations/Ber/NumberedEquation4.gif) |
(4) |
where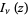 
is a modified Bessel function of the first kind.
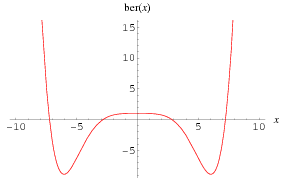
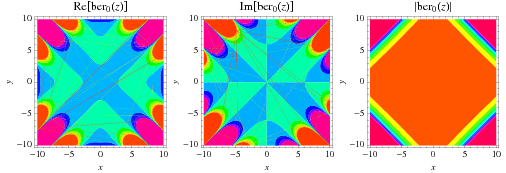
The special case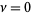 
, commonly denoted 
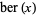, corresponds to
 |
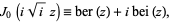(5) |
where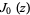 
is the zeroth order Bessel function of the first kind. The function 
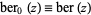has the series expansion
![ber(z)=1+sum_(n=1)^infty((-1)^n(1/2z)^(4n))/([(2n)!]^2)](http://mathworld.wolfram.com/images/equations/Ber/NumberedEquation6.gif) |
(6) |
which can be written in closed form as
 |
 |
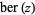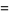![1/2[I_0((-1)^(1/4)z)+J_0((-1)^(1/4)z)]](http://mathworld.wolfram.com/images/equations/Ber/Inline13.gif) |
(7) |
 |
 |
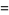![1/2[I_0((-1)^(1/4)z)+I_0((-1)^(3/4)z)].](http://mathworld.wolfram.com/images/equations/Ber/Inline16.gif) |
(8) |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Kelvin Functions." §9.9 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 379-381, 1972.
Prudnikov, A. P.; Marichev, O. I.; and Brychkov, Yu. A. "The Kelvin Functions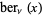 
, 
, 
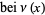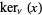and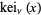 
." §1.7 in Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach, pp. 29-30, 1990.
Spanier, J. and Oldham, K. B. "The Kelvin Functions." Ch. 55 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 543-554, 1987.
|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
مشاتل الكفيل تزيّن مجمّع أبي الفضل العبّاس (عليه السلام) بالورد استعدادًا لحفل التخرج المركزي
|
|
|
