Infimum

The infimum is the greatest lower bound of a set 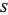, defined as a quantity  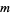such that no member of the set is less than 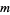, but if  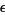is any positive quantity, however small, there is always one member that is less than  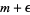(Jeffreys and Jeffreys 1988). When it exists (which is not required by this definition, e.g.,  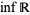does not exist), the infimum is denoted  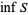or 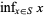. The infimum is implemented in the Wolfram Language as MinValue[f, constr, vars].

Consider the real numbers with their usual order. Then for any set 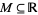, the infimum  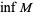exists (in 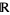) if and only if  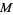is bounded from below and nonempty.

More formally, the infimum 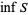 for 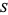 a (nonempty) subset of the affinely extended real numbers  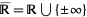is the largest value  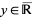such that for all  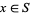we have 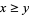. Using this definition,  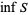always exists and, in particular, .

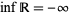Whenever an infimum exists, its value is unique.

REFERENCES:

Croft, H. T.; Falconer, K. J.; and Guy, R. K. Unsolved Problems in Geometry. New York: Springer-Verlag, p. 2, 1991.

Jeffreys, H. and Jeffreys, B. S. "Upper and Lower Bounds." §1.044 in Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, p. 13, 1988.

Knopp, K. Theory of Functions Parts I and II, Two Volumes Bound as One, Part I. New York: Dover, p. 6, 1996.

Royden, H. L. Real Analysis, 3rd ed. New York: Macmillan, p. 31, 1988.

Rudin, W. Real and Complex Analysis, 3rd ed. New York: McGraw-Hill, p. 7, 1987.