


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 15-6-2019
Date: 5-9-2019
Date: 30-9-2019
|
The arithmetic-geometric mean 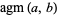 of two numbers
of two numbers 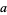 and
and 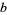 (often also written
(often also written 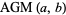 or
or 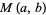 ) is defined by starting with
) is defined by starting with 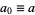 and
and 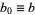 , then iterating
, then iterating
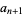 |
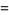 |
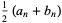 |
(1) |
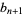 |
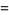 |
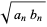 |
(2) |
until 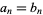 to the desired precision.
to the desired precision.
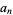 and
and 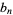 converge towards each other since
converge towards each other since
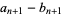 |
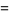 |
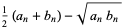 |
(3) |
 |
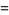 |
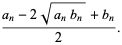 |
(4) |
But 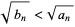 , so
, so
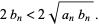 |
(5) |
Now, add 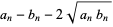 to each side
to each side
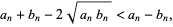 |
(6) |
so
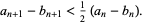 |
(7) |
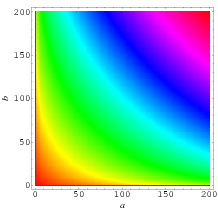 |
 |
The top plots show  for
for 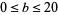 and
and 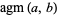 for
for 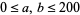 , while the bottom two plots show
, while the bottom two plots show 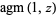 for complex values of
for complex values of 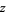 .
.
The AGM is very useful in computing the values of complete elliptic integrals and can also be used for finding the inverse tangent.
It is implemented in the Wolfram Language as ArithmeticGeometricMean[a, b].
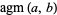 can be expressed in closed form in terms of the complete elliptic integral of the first kind
can be expressed in closed form in terms of the complete elliptic integral of the first kind 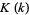 as
as
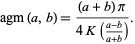 |
(8) |
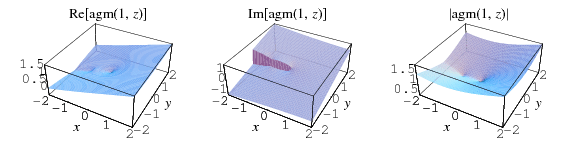
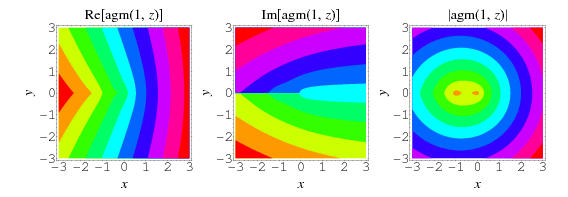
The definition of the arithmetic-geometric mean also holds in the complex plane, as illustrated above for 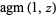 .
.
The Legendre form of the arithmetic-geometric mean is given by
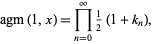 |
(9) |
where 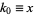 and
and
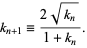 |
(10) |
Special values of  are summarized in the following table. The special value
are summarized in the following table. The special value
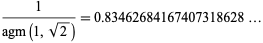 |
(11) |
(OEIS A014549) is called Gauss's constant. It has the closed form
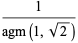 |
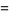 |
 |
(12) |
 |
 |
![([Gamma(1/4)]^2)/(2pi^(3/2)sqrt(2))](http://mathworld.wolfram.com/images/equations/Arithmetic-GeometricMean/Inline41.gif) |
(13) |
where the above integral is the lemniscate function and the equality of the arithmetic-geometric mean to this integral was known to Gauss (Borwein and Bailey 2003, pp. 13-15).
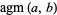 |
Sloane | value |
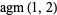 |
A068521 | 1.4567910310469068692... |
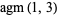 |
A084895 | 1.8636167832448965424... |
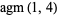 |
A084896 | 2.2430285802876025701... |
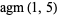 |
A084897 | 2.6040081905309402887... |
The derivative of the AGM is given by
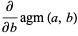 |
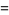 |
![(agm(a,b))/((a-b)bpi)[2agm(a,b)E(k)-bpi]](http://mathworld.wolfram.com/images/equations/Arithmetic-GeometricMean/Inline49.gif) |
(14) |
 |
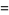 |
![pi/(8kb)((a+b)E(k)-2bK(k))/([K(k)]^2),](http://mathworld.wolfram.com/images/equations/Arithmetic-GeometricMean/Inline52.gif) |
(15) |
where 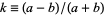 ,
, 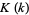 is a complete elliptic integral of the first kind, and
is a complete elliptic integral of the first kind, and 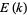 is the complete elliptic integral of the second kind.
is the complete elliptic integral of the second kind.
A series expansion for 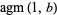 is given by
is given by
![agm(1,b)=-pi/(2ln(1/4b))+(pi[1+ln(1/4b)]b^2)/(8[ln(1/4b)]^2)+O(b^4).](http://mathworld.wolfram.com/images/equations/Arithmetic-GeometricMean/NumberedEquation8.gif) |
(16) |
The AGM has the properties
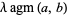 |
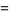 |
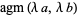 |
(17) |
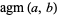 |
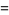 |
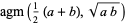 |
(18) |
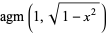 |
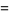 |
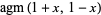 |
(19) |
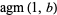 |
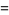 |
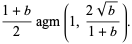 |
(20) |
Solutions to the differential equation
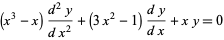 |
(21) |
are given by ![[agm(1+x,1-x)]^(-1)](http://mathworld.wolfram.com/images/equations/Arithmetic-GeometricMean/Inline69.gif) and
and ![[agm(1,x)]^(-1)](http://mathworld.wolfram.com/images/equations/Arithmetic-GeometricMean/Inline70.gif) .
.
A generalization of the arithmetic-geometric mean is
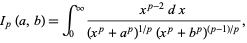 |
(22) |
which is related to solutions of the differential equation
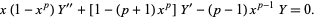 |
(23) |
The case 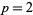 corresponds to the arithmetic-geometric mean via
corresponds to the arithmetic-geometric mean via
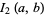 |
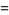 |
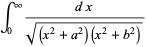 |
(24) |
 |
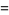 |
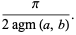 |
(25) |
The case 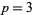 gives the cubic relative
gives the cubic relative
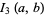 |
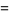 |
![int_0^infty(xdx)/([(a^3+x^3)(b^3+x^3)^2]^(1/3))](http://mathworld.wolfram.com/images/equations/Arithmetic-GeometricMean/Inline81.gif) |
(26) |
 |
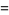 |
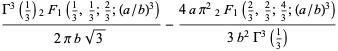 |
(27) |
discussed by Borwein and Borwein (1990, 1991) and Borwein (1996). For 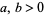 , this function satisfies the functional equation
, this function satisfies the functional equation
![I_3(a,b)=I_3((a+2b)/3,[b/3(a^2+ab+b^2)]^(1/3)).](http://mathworld.wolfram.com/images/equations/Arithmetic-GeometricMean/NumberedEquation12.gif) |
(28) |
It therefore turns out that for iteration with 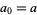 and
and 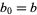 and
and
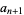 |
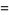 |
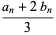 |
(29) |
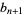 |
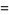 |
![[(b_n)/3(a_n^2+a_nb_n+b_n^2)]^(1/3),](http://mathworld.wolfram.com/images/equations/Arithmetic-GeometricMean/Inline93.gif) |
(30) |
so
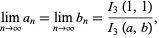 |
(31) |
where
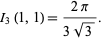 |
(32) |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "The Process of the Arithmetic-Geometric Mean." §17.6 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 571 and 598-599, 1972.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
Borwein, J. M. Problem 10281. "A Cubic Relative of the AGM." Amer. Math. Monthly 103, 181-183, 1996.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987.
Borwein, J. M. and Borwein, P. B. "A Remarkable Cubic Iteration." In Computational Method & Function Theory: Proc. Conference Held in Valparaiso, Chile, March 13-18, 1989 (Ed. A. Dold, B. Eckmann, F. Takens, E. B. Saff, S. Ruscheweyh, L. C. Salinas, and R. S. Varga). New York: Springer-Verlag, 1990.
Borwein, J. M. and Borwein, P. B. "A Cubic Counterpart of Jacobi's Identity and the AGM." Trans. Amer. Math. Soc. 323, 691-701, 1991.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 906-907, 1992.
Sloane, N. J. A. Sequences A014549, A068521, A084895, A084896, and A084897 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
معهد الكفيل للنطق والتأهيل: أطلقنا برامج متنوعة لدعم الأطفال وتعزيز مهاراتهم التعليمية والاجتماعية
|
|
|