Dixon,s Theorem
المؤلف:
Bailey, W. N.
المصدر:
"Dixon,s Theorem." §3.1 in Generalised Hypergeometric Series. Cambridge, England: Cambridge University Press
الجزء والصفحة:
...
15-6-2019
3671
Dixon's Theorem
![_3F_2[n,-x,-y; x+n+1,y+n+1]
=Gamma(x+n+1)Gamma(y+n+1)Gamma(1/2n+1)Gamma(x+y+1/2n+1)
×Gamma(n+1)Gamma(x+y+n+1)Gamma(x+1/2n+1)Gamma(y+1/2n+1),](http://mathworld.wolfram.com/images/equations/DixonsTheorem/NumberedEquation1.gif) |
(1)
|
where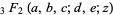 
is a generalized hypergeometric function and 
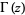is the gamma function. It can be derived from the Dougall-Ramanujan identity. It can be written more symmetrically as
 |
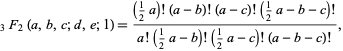(2)
|
where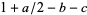 
has a positive real part, 
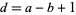, and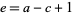 
(Bailey 1935, p. 13; Petkovšek et al. 1996; Koepf 1998, p. 32). The identity can also be written as the beautiful symmetric sum
 |
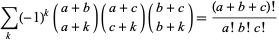(3)
|
(Petkovšek et al. 1996). In this form, it closely resembles Dixon's identity.
REFERENCES:
Bailey, W. N. "Dixon's Theorem." §3.1 in Generalised Hypergeometric Series. Cambridge, England: Cambridge University Press, pp. 13-14, 1935.
Cartier, P. and Foata, D. Problèmes combinatoires de commutation et réarrangements. New York: Springer-Verlag, 1969.
Dixon, A. C. "On the Sum of the Cubes of the Coefficients in Certain Expansion by the Binomial Theorem." Messenger Math. 20, 79-80, 1891.
Dixon, A. C. "Summation of Certain Series." Proc. London Math. Soc. 35, 285-289, 1903.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, pp. 104 and 111, 1999.
Knuth, D. E. The Art of Computer Programming, Vol. 1: Fundamental Algorithms, 3rd ed. Reading, MA: Addison-Wesley, 1997.
Koepf, W. Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, pp. 18-19, 1998.
MacMahon P. A. "The Sums of the Powers of the Binomial Coefficients." Quart. J. Math. 33, 274-288, 1902.
Morley, F. "On the Series ![1+(p/1)^3+<span style=]()
{(p(p+1))/(1·2)}^2+..." src="http://mathworld.wolfram.com/images/equations/DixonsTheorem/Inline6.gif" style="height:25px; width:141px" />." Proc. London Math. Soc. 34, 397-402, 1902.
Petkovšek, M.; Wilf, H. S.; and Zeilberger, D. A=B. Wellesley, MA: A K Peters, p. 43, 1996. http://www.cis.upenn.edu/~wilf/AeqB.html.
Richmond, H. W. "The Sum of the Cubes of the Coefficients in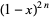 
." Messenger Math. 21, 77-78, 1892.
Watson, G. N. "Dixon's Theorem on Generalized Hypergeometric Functions." Proc. London Math. Soc. 22, xxxii-xxxiii (Records for 17 May, 1923), 1924.
Zeilberger, D. and Bressoud, D. "A Proof of Andrews'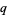 
-Dyson Conjecture." Disc. Math. 54, 201-224, 1985.
الاكثر قراءة في التفاضل و التكامل
اخر الاخبار
اخبار العتبة العباسية المقدسة
