Quartic Equation

A quartic equation is a fourth-order polynomial equation of the form

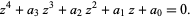(1)

While some authors (Beyer 1987b, p. 34) use the term "biquadratic equation" as a synonym for quartic equation, others (Hazewinkel 1988, Gellert et al. 1989) reserve the term for a quartic equation having no cubic term, i.e., a quadratic equation in .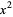

Ferrari was the first to develop an algebraic technique for solving the general quartic, which was stolen and published in Cardano's Ars Magna in 1545 (Boyer and Merzbach 1991, p. 283). The Wolfram Language can solve quartic equations exactly using the built-in command Solve[a4 x^4 + a3 x^3 + a2 x^2 + a1 x + a0 == 0, x]. The solution can also be expressed in terms of Wolfram Language algebraic root objects by first issuing SetOptions[Roots, Quartics -> False].

The roots of this equation satisfy Vieta's formulas:

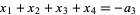	(2)
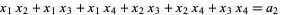	(3)
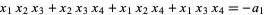	(4)
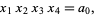	(5)

where the denominators on the right side are all 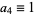. Writing the quartic in the standard form

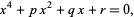(6)

the properties of the symmetric polynomials appearing in Vieta's formulas then give

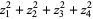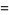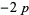			(7)
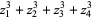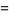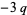			(8)
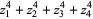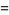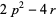			(9)
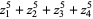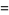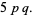			(10)

Eliminating 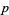, , 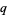and 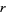, respectively, gives the relations

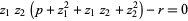(11)

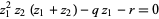(12)

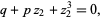(13)

as well as their cyclic permutations.

Ferrari was the first to develop an algebraic technique for solving the general quartic. He applied his technique (which was stolen and published by Cardano) to the equation

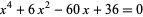(14)

(Smith 1994, p. 207).

The 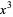 term can be eliminated from the general quartic (◇) by making a substitution of the form

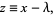(15)

so

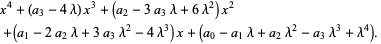(16)

Letting 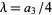 so

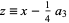(17)

then gives the standard form

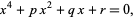(18)

where

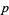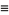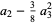			(19)
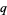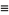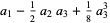			(20)
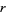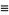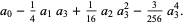			(21)

The quartic can be solved by writing it in a general form that would allow it to be algebraically factorable and then finding the condition to put it in this form. The equation that must be solved to make it factorable is called the resolvent cubic. To do this, note that the quartic will be factorable if it can be written as the difference of two squared terms,

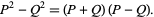(22)

It turns out that a factorization of this form can be obtained by adding and subtracting 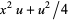 (where  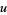is for now an arbitrary quantity, but which will be specified shortly) to equation (◇) to obtain

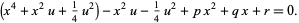(23)

This equation can be rewritten

(24)

(Birkhoff and Mac Lane 1966). Note that the first term is immediately a perfect square 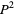 with

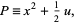(25)

and the second term will be a perfect square 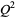 if 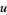 is chosen to that the square can be completed in

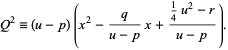(26)

This means we want

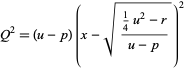(27)

which requires that

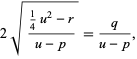(28)

or

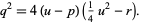(29)

This is the resolvent cubic.

Since an analytic solution to the cubic is known, we can immediately solve algebraically for one of the three solution of equation (29), say 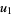, and plugging equation (29) into equation (26) then gives

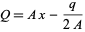(30)

with

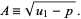(31)

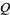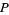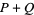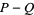 therefore is linear in  and  is quadratic in , so each term  and  is quadratic and can be solved using the quadratic formula, thus giving all four solutions to the original quartic.

Explicitly, plugging 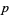, , 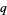and 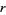 back into (◇) gives

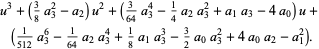(32)

This can be simplified by making the substitution

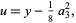(33)

which gives the resolvent cubic equation

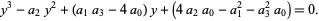(34)

Let 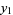 be a real root of (34), then the four roots of the original quartic are given by the roots of the equation

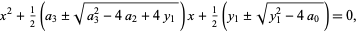(35)

which are

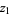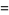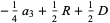			(36)
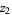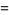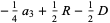			(37)
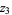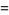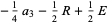			(38)
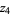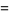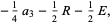			(39)

where

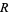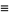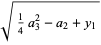			(40)
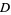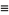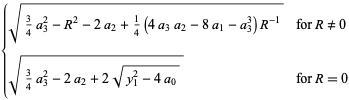			(41)
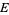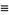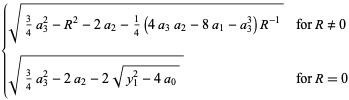			(42)

(Abramowitz and Stegun 1972, p. 17; Beyer 1987, p. 12).

Another approach to solving the quartic (◇) defines

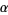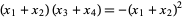			(43)
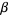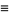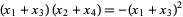			(44)
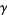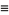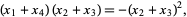			(45)

where the second forms follow from

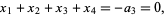(46)

and defining

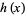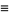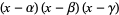			(47)
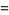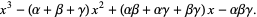			(48)

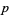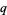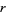This equation can be written in terms of the original coefficients , , and  as

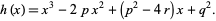(49)

The roots of this cubic equation then give 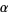, , 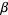and 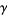, and the equations (◇) to (◇) can be solved for the four roots 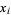of the original quartic (Faucette 1996).

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Solutions of Quartic Equations." §3.8.3 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 17-18, 1972.

Berger, M. §16.4.1-16.4.11.1 in Geometry I. New York:Springer-Verlag, 1987.

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 12, 1987a.

Beyer, W. H. Handbook of Mathematical Sciences, 6th ed. Boca Raton, FL: CRC Press, 1987b.

Birkhoff, G. and Mac Lane, S. A Survey of Modern Algebra, 5th ed. New York: Macmillan, pp. 107-108, 1996.

Borwein, P. and Erdélyi, T. "Quartic Equations." §1.1.E.1e in Polynomials and Polynomial Inequalities. New York:Springer-Verlag, p. 4, 1995.

Boyer, C. B. and Merzbach, U. C. A History of Mathematics, 2nd ed. New York: Wiley, pp. 286-287, 1991.

Ehrlich, G. §4.16 in Fundamental Concepts of Abstract Algebra. Boston, MA: PWS-Kent, 1991.

Faucette, W. M. "A Geometric Interpretation of the Solution of the General Quartic Polynomial." Amer. Math. Monthly 103, 51-57, 1996.

Gellert, W.; Gottwald, S.; Hellwich, M.; Kästner, H.; and Künstner, H. (Eds.). VNR Concise Encyclopedia of Mathematics, 2nd ed.New York: Van Nostrand Reinhold, 1989.

Hazewinkel, M. (Managing Ed.). Encyclopaedia of Mathematics: An Updated and Annotated Translation of the Soviet "Mathematical Encyclopaedia." Dordrecht, Netherlands: Reidel, 1988.

MathPages. "Reducing Quartics to Cubics." http://www.mathpages.com/home/kmath296.htm.

Smith, D. E. A Source Book in Mathematics. New York: Dover, 1994.

van der Waerden, B. L. §64 in Algebra, Vol. 1. New York:Springer-Verlag, 1993.