


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-3-2019
Date: 23-1-2019
Date: 13-2-2019
|
A map defined by one or more polynomials. Given a field 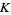 , a polynomial map is a map
, a polynomial map is a map 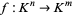 such that for all points
such that for all points 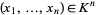 ,
,
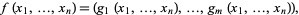 |
for suitable polynomials ![g_1,...,g_m in K[X_1,...,X_n]](http://mathworld.wolfram.com/images/equations/PolynomialMap/Inline4.gif) . The zero set of
. The zero set of 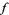 is the set of all solutions of the simultaneous equations
is the set of all solutions of the simultaneous equations 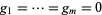 , and is an algebraic variety in
, and is an algebraic variety in 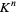 .
.
An example of polynomial map is the 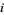 th coordinate map
th coordinate map 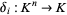 , defined by
, defined by 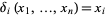 for all
for all 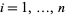 . In the language of set theory, it is the projection of the Cartesian product
. In the language of set theory, it is the projection of the Cartesian product 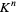 onto the
onto the 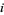 th factor.
th factor.
Polynomial maps can be defined on any nonempty subset 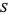 of
of 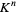 . If
. If 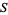 is an affine variety, then the set of all polynomial maps from
is an affine variety, then the set of all polynomial maps from 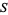 to
to 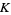 is the coordinate ring
is the coordinate ring ![K[S]](http://mathworld.wolfram.com/images/equations/PolynomialMap/Inline19.gif) of
of 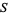 . If
. If 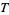 is an affine variety of
is an affine variety of 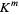 , then every polynomial map
, then every polynomial map 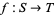 induces a ring homomorphism
induces a ring homomorphism ![F:K[T]->K[S]](http://mathworld.wolfram.com/images/equations/PolynomialMap/Inline24.gif) , defined by
, defined by 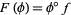 . Conversely, every ring homomorphism
. Conversely, every ring homomorphism ![G:K[T]->K[S]](http://mathworld.wolfram.com/images/equations/PolynomialMap/Inline26.gif) determines a polynomial map
determines a polynomial map 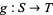 , where
, where 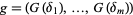 .
.
A polynomial map 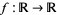 is a real-valued polynomial function. Its graph is the plane algebraic curve with Cartesian equation
is a real-valued polynomial function. Its graph is the plane algebraic curve with Cartesian equation 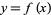 .
.
REFERENCES:
Becker, T. and Weispfenning, V. Gröbner Bases: A Computational Approach to Commutative Algebra. New York: Springer-Verlag, p. 330, 1993.



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
|
|
|