Icosahedral Equation

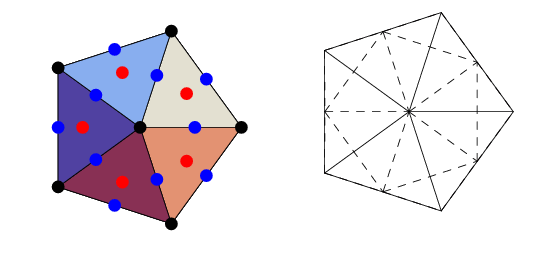
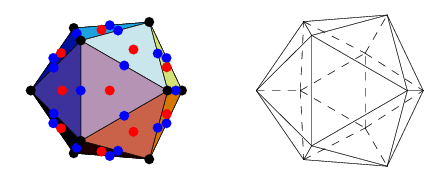
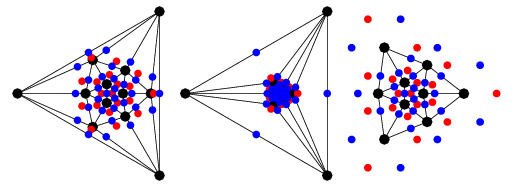
There are a number of algebraic equations known as the icosahedral equation, all of which derive from the projective geometry of the icosahedron. Consider an icosahedron centered 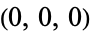, oriented with 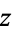-axis along a fivefold () rotational symmetry axis, and with one of the top five edges lying in the 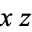-plane (left figure). In this figure, vertices are shown in black, face centers in red, and edge midpoints in blue.

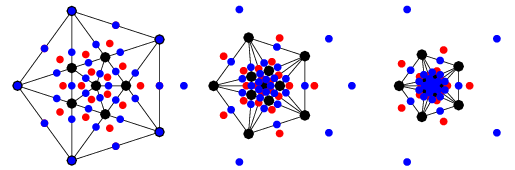
The simplest icosahedral equation is defined by projecting the vertices of the icosahedron with unit circumradius using a stereographic projection from the south pole of its circumsphere onto the plane 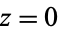, and expressing these vertex locations (interpreted as complex quantities in the complex 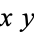-plane) as roots of an algebraic equation. The resulting projection is shown as the left figure above, with black dots being the vertex positions. The resulting equation is

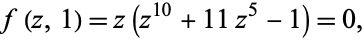(1)

where 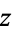 here refers to the coordinate in the complex plane (not the height above the projection plane), and the equation is of order 11 instead of 12 since the vertex at  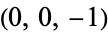is transformed to infinity and has been omitted. Writing the above equation in symmetric form gives

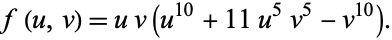(2)

If the icosahedron with unit inradius is instead projected (second figure above), the equation expressing the positions of the face centers (red dots) is given by

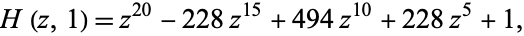(3)

or in symmetric form,

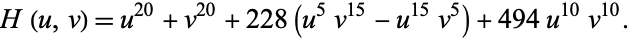(4)

Finally, if the icosahedron with unit midradius is projected (right figure above), the equation expressing the positions of the edge midpoints (blue dots) is given by

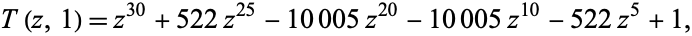(5)

or in symmetric form,

(6)

Note that because these equations involve variables to multiples of the power 5, rotating the solid by 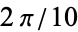 radians changes transforms the quantities from  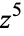to 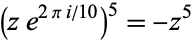, producing the same equations modulo minus signs in odd powers of 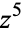, corresponding to flipping the positions of the roots about the imaginary axis.

Combining  and 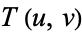 gives a general equation commonly known as "the" icosahedral equation,

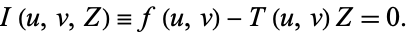(7)

Hunt (1996) considers a "dehomogenized" icosahedral equation given by

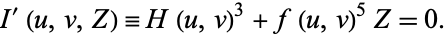(8)

If the icosahedron is instead oriented so that the top and bottom faces are parallel to the -plane, the corresponding equation giving its projected vertices is

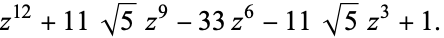(9)

REFERENCES:

Crass, S. "Solving the Quintic by Iteration in Three Dimensions" 9 Mar 1999. http://arxiv.org/abs/math.DS/9903054.

Doyle, P. and McMullen, C. "Solving the Quintic by Iteration." Acta Math. 163, 151-180, 1989.

Fricke, R. Lehrbuch der Algebra, Vol. 2. Braunschweig, Germany: Vieweg, 1926.

Hunt, B. The Geometry of Some Special Arithmetic Quotients. New York: Springer-Verlag, p. 146, 1996.

King, R. B. and Cranfield, E. R. Comput. Math. Appl. 24, 13, 1992.

Klein, F. "Further Investigations on the Icosahedron." Math. Ann. 121, 503, 1877.

Klein, F. "Sull' equazione dell' Icosaedro nella risoluzione delle equazioni del quinto grado [per funzioni ellittiche]." Reale Istituto Lombardo, Rendiconto, Ser. 2 10, 1877.

Klein, F. Lectures on the Icosahedron and the Solution of Equations of the Fifth Degree. New York: Dover, 1956. Republished with commentaries by P. Slodowy, Basel: Birkhäuser, 1993.

Magot, N. and Zvonkin, A. "Belyi Functions for Archimedean Solids." Disc. Math. 217, 249-271, 2000.

McKean, H. and Moll, V. Elliptic Curves: Function Theory, Geometry, Arithmetic. Cambridge, England: Cambridge University Press, 1997.

Trott, M. "Solution of Quintics with Hypergeometric Functions." §3.13 in The Mathematica GuideBook for Symbolics. New York: Springer-Verlag, 2005.