


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 1-11-2018
Date: 18-11-2018
Date: 24-10-2018
|
The constant 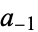 in the Laurent series
in the Laurent series
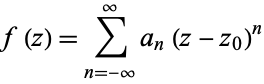 |
(1) |
of 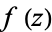 about a point
about a point 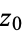 is called the residue of
is called the residue of 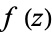 . If
. If 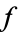 is analytic at
is analytic at 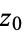 , its residue is zero, but the converse is not always true (for example,
, its residue is zero, but the converse is not always true (for example, 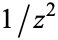 has residue of 0 at
has residue of 0 at 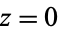 but is not analytic at
but is not analytic at 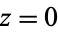 ). The residue of a function
). The residue of a function 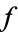 at a point
at a point 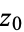 may be denoted
may be denoted 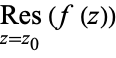 . The residue is implemented in the Wolfram Language as Residue[f,
. The residue is implemented in the Wolfram Language as Residue[f, 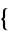 z, z0
z, z0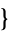 ].
].
Two basic examples of residues are given by 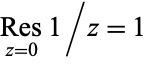 and
and 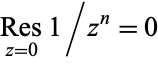 for
for 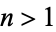 .
.
The residue of a function 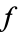 around a point
around a point 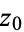 is also defined by
is also defined by
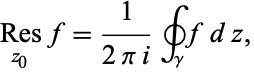 |
(2) |
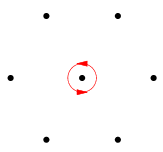
where 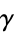 is counterclockwise simple closed contour, small enough to avoid any other poles of
is counterclockwise simple closed contour, small enough to avoid any other poles of 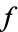 . In fact, any counterclockwise path with contour winding number 1 which does not contain any other poles gives the same result by the Cauchy integral formula. The above diagram shows a suitable contour for which to define the residue of function, where the poles are indicated as black dots.
. In fact, any counterclockwise path with contour winding number 1 which does not contain any other poles gives the same result by the Cauchy integral formula. The above diagram shows a suitable contour for which to define the residue of function, where the poles are indicated as black dots.
It is more natural to consider the residue of a meromorphic one-form because it is independent of the choice of coordinate. On a Riemann surface, the residue is defined for a meromorphic one-form 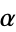 at a point
at a point 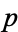 by writing
by writing 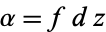 in a coordinate
in a coordinate 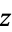 around
around 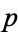 . Then
. Then
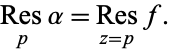 |
(3) |
The sum of the residues of 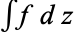 is zero on the Riemann sphere. More generally, the sum of the residues of a meromorphic one-form on a compact Riemann surface must be zero.
is zero on the Riemann sphere. More generally, the sum of the residues of a meromorphic one-form on a compact Riemann surface must be zero.
The residues of a function 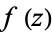 may be found without explicitly expanding into a Laurent series as follows. If
may be found without explicitly expanding into a Laurent series as follows. If 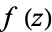 has a pole of order
has a pole of order 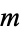 at
at 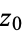 , then
, then 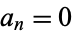 for
for 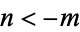 and
and 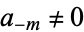 . Therefore,
. Therefore,
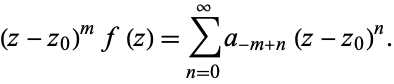 |
(4) |
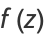 |
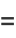 |
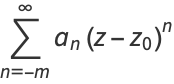 |
(5) |
![d/(dz)[(z-z_0)^mf(z)]](http://mathworld.wolfram.com/images/equations/ComplexResidue/Inline38.gif) |
 |
 |
(6) |
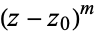 |
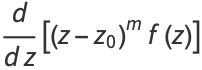 |
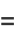 |
(7) |
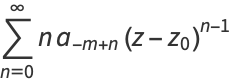 |
 |
 |
(8) |
![(d^2)/(dz^2)[(z-z_0)^mf(z)]](http://mathworld.wolfram.com/images/equations/ComplexResidue/Inline47.gif) |
 |
 |
(9) |
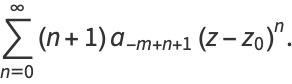 |
 |
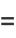 |
(10) |
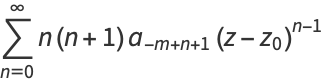 |
 |
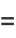 |
(11) |
Iterating,
![(d^(m-1))/(dz^(m-1))[(z-z_0)^mf(z)]=sum_(n=0)^infty(n+1)(n+2)...(n+m-1)a_(n-1)(z-z_0)^n
=(m-1)!a_(-1)+sum_(n=1)^infty(n+1)(n+2)...(n+m-1)a_(n-1)(z-z_0)^(n-1).](http://mathworld.wolfram.com/images/equations/ComplexResidue/NumberedEquation5.gif) |
(12) |
So
![lim_(z->z_0)(d^(m-1))/(dz^(m-1))[(z-z_0)^mf(z)]](http://mathworld.wolfram.com/images/equations/ComplexResidue/Inline56.gif) |
 |
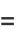 |
(13) |
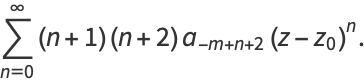 |
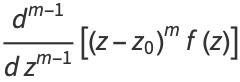 |
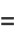 |
(14) |
and the residue is
![a_(-1)=1/((m-1)!)(d^(m-1))/(dz^(m-1))[(z-z_0)^mf(z)]_(z=z_0).](http://mathworld.wolfram.com/images/equations/ComplexResidue/NumberedEquation6.gif) |
(15) |
The residues of a holomorphic function at its poles characterize a great deal of the structure of a function, appearing for example in the amazing residue theorem of contour integration.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|