A Gaussian integer is a complex number 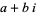 where 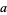 and 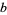 are integers. The Gaussian integers are members of the imaginary quadratic field  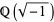and form a ring often denoted , or sometimes 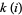 (Hardy and Wright 1979, p. 179). The sum, difference, and product of two Gaussian integers are Gaussian integers, but  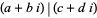only if there is an  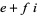such that

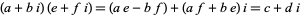(1)

(Shanks 1993).

Gaussian integers can be uniquely factored in terms of other Gaussian integers (known as Gaussian primes) up to powers of 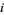 and rearrangements.

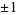The units of  are  and .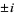

One definition of the norm of a Gaussian integer is its complex modulus

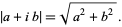(2)

Another common definition (e.g., Herstein 1975; Hardy and Wright 1979, p. 182; Artin 1991; Dummit and Foote 2004) defines the norm of a Gaussian integer to be

(3)

the square of the above quantity. (Note that the Gaussian integers form a Euclidean ring, which is what makes them particularly of interest, only under the latter definition.) Because of the two possible definitions, caution is needed when consulting the literature.

The probability that two Gaussian integers  and  are relatively prime is

(4)

(OEIS A088454), where 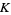 is Catalan's constant (Pegg; Collins and Johnson 1989; Finch 2003, p. 601).

Every Gaussian integer is within 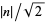 of a multiple of a Gaussian integer .

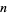The plots above show roots  of the Gaussian integers for various rational values of 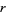 (Trott 2004, p. 24).

REFERENCES:

Artin, M. Algebra. Englewood Cliffs, NJ: Prentice-Hall, 1991.

Collins, G. E. and Johnson, J. R. "The Probability of Relative Primality of Gaussian Integers." Proc. 1988 Internat. Sympos. Symbolic and Algebraic Computation (ISAAC), Rome (Ed. P. Gianni). New York: Springer-Verlag, pp. 252-258, 1989.

Conway, J. H. and Guy, R. K. "Gauss's Whole Numbers." In The Book of Numbers. New York: Springer-Verlag, pp. 217-223, 1996.

Dummit, D. S. and Foote, R. M. Abstract Algebra, 3rd ed. Englewood Cliffs, NJ: Prentice-Hall, 2004.

Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, 2003.

Hardy, G. H. and Wright, E. M. "The Rational Integers, the Gaussian Integers, and the Integers of 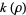" and "Properties of the Gaussian Integers." §12.2 and 12.6 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 178-180 and 182-183, 1979.

Herstein, I. N. Topics in Algebra, 2nd ed. New York: Springer-Verlag, 1975.

Pegg, E. Jr. "The Neglected Gaussian Integers." http://www.mathpuzzle.com/Gaussians.html.

Séroul, R. "The Gaussian Integers." §9.1 in Programming for Mathematicians. Berlin: Springer-Verlag, pp. 225-234, 2000.

Shanks, D. "Gaussian Integers and Two Applications." §50 in Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 149-151, 1993.

Sloane, N. J. A. Sequence A088454 in "The On-Line Encyclopedia of Integer Sequences."

Trott, M. The Mathematica GuideBook for Graphics. New York: Springer-Verlag, 2004. http://www.mathematicaguidebooks.org/.

اخر الاخبار

اخبار العتبة العباسية المقدسة

عباس.. طفل فقد والده فوجد في خدمة زائري عاشوراء وطنًا آمنًا

شعبة الخطابة النسوية تواصل إقامة مجالس العزاء في شهر المحرم الحرام

لليوم الخامس.. العتبة العباسية المقدسة تقيم مجلس عزاء في صحن مرقد أبي الفضل العباس (عليه السلام)

قسم الشؤون الفكرية يقيم مجلس عزاء حسيني في العاصمة التنزانية دار السلام

المزيد

الآخبار الصحية

لمن تجاوز الستين.. عليك بشرب 4 أكواب من القهوة يوميا ؟

الحليب مع العسل.. مزيج يمنحك 7 فوائد صحية

لا تبالغ في التنظيف.. قليل من "الاتساخ" قد يحمي عائلتك

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

المزيد

الآخبار التكنلوجية

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

المزيد