المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Blaschke Factorization |
 352
 01:16 مساءً
date: 27-11-2018 |
Author : Krantz, S. G 
Book or Source : "Blaschke Factorization." §9.1.7 in Handbook of Complex Variables. Boston, MA: Birkhäuser 
Page and Part : p. 119|
Read More
Date: 16-12-2018
476
Date: 28-11-2018
424
Date: 27-11-2018
1313
|
Let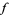 
be a bounded analytic function on 
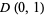vanishing to order 
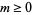at 0 and let 
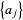be its other zeros, listed with multiplicities. Then
 |
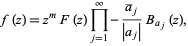where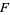 
is a bounded analytic function on 
, 
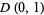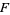is zerofree, 
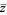is the complex conjugate, and
 |
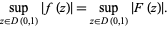REFERENCES:
Krantz, S. G. "Blaschke Factorization." §9.1.7 in Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 119, 1999.
|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|
