المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Hadamard Factorization Theorem |
 422
 02:08 مساءً
date: 28-11-2018 |
Author : Krantz, S. G 
Book or Source : The Hadamard Factorization Theorem." §9.3.5 in Handbook of Complex Variables. Boston, MA: Birkhäuser 
Page and Part : pp. 121-122|
Read More
Date: 14-10-2018
378
Date: 18-12-2018
514
Date: 24-10-2018
408
|
Let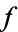 
be an entire function of finite order 
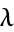and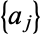 
the zeros of 
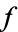, listed with multiplicity, then the rank 
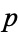of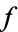 
is defined as the least positive integer such that
 |
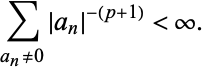(1) |
Then the canonical Weierstrass product is given by
 |
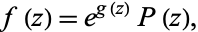(2) |
and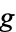 
has degree 
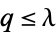. The genus 
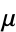of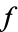 
is then defined as 
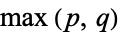, and the Hadamard factorization theory states that an entire function of finite order 
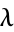is also of finite genus 
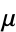, and
 |
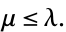(3) |
REFERENCES:
Krantz, S. G. "The Hadamard Factorization Theorem." §9.3.5 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 121-122, 1999.
|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|
