


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-7-2018
Date: 12-7-2018
Date: 21-7-2018
|
A determinant used to determine in which coordinate systems the Helmholtz differential equation is separable (Morse and Feshbach 1953). A determinant
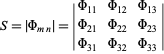 |
(1) |
in which 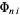 are functions of
are functions of 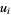 alone is called a Stäckel determinant. A coordinate system is separable if it obeys the Robertson condition, namely that the scale factors
alone is called a Stäckel determinant. A coordinate system is separable if it obeys the Robertson condition, namely that the scale factors 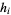 in the Laplacian
in the Laplacian
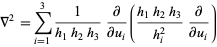 |
(2) |
can be rewritten in terms of functions 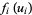 defined by
defined by
![1/(h_1h_2h_3)partial/(partialu_i)((h_1h_2h_3)/(h_i^2)partial/(partialu_i))
=(g(u_(i+1),u_(i+2)))/(h_1h_2h_3)partial/(partialu_i)[f_i(u_i)partial/(partialu_i)]
=1/(h_i^2f_i)partial/(partialu_i)(f_ipartial/(partialu_i))](http://mathworld.wolfram.com/images/equations/StaeckelDeterminant/NumberedEquation3.gif) |
(3) |
such that 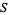 can be written
can be written
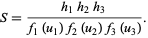 |
(4) |
When this is true, the separated equations are of the form
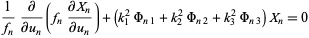 |
(5) |
The 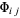 s obey the minor equations
s obey the minor equations
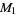 |
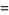 |
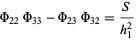 |
(6) |
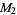 |
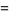 |
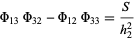 |
(7) |
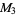 |
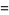 |
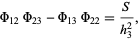 |
(8) |
which are equivalent to
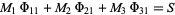 |
(9) |
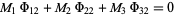 |
(10) |
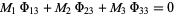 |
(11) |
(Morse and Feshbach 1953, p. 509). This gives a total of four equations in nine unknowns. Morse and Feshbach (1953, pp. 655-666) give not only the Stäckel determinants for common coordinate systems, but also the elements of the determinant (although it is not clear how these are derived).
REFERENCES:
Moon, P. and Spencer, D. E. Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions, 2nd ed. New York: Springer-Verlag, pp. 5-7, 1988.
Morse, P. M. and Feshbach, H. "Tables of Separable Coordinates in Three Dimensions." Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 509-511 and 655-666, 1953.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|