


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-12-2018
Date: 11-6-2018
Date: 22-6-2018
|
A Lyapunov function is a scalar function 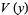 defined on a region
defined on a region 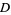 that is continuous, positive definite,
that is continuous, positive definite, 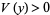 for all
for all 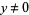 ), and has continuous first-order partial derivatives at every point of
), and has continuous first-order partial derivatives at every point of 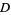 . The derivative of
. The derivative of 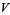 with respect to the system
with respect to the system 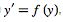 , written as
, written as 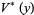 is defined as the dot product
is defined as the dot product
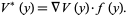 |
(1) |
The existence of a Lyapunov function for which 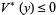 on some region
on some region 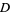 containing the origin, guarantees the stability of the zero solution of
containing the origin, guarantees the stability of the zero solution of 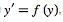 , while the existence of a Lyapunov function for which
, while the existence of a Lyapunov function for which 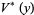 is negative definite on some region
is negative definite on some region 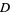 containing the origin guarantees the asymptotical stability of the zero solution of
containing the origin guarantees the asymptotical stability of the zero solution of  .
.
For example, given the system
 |
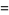 |
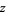 |
(2) |
 |
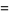 |
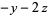 |
(3) |
and the Lyapunov function 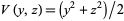 , we obtain
, we obtain
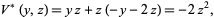 |
(4) |
which is nonincreasing on every region containing the origin, and thus the zero solution is stable.
REFERENCES:
Boyce, W. E. and DiPrima, R. C. Elementary Differential Equations and Boundary Value Problems, 5th ed. New York: Wiley, pp. 502-512, 1992.
Brauer, F. and Nohel, J. A. The Qualitative Theory of Ordinary Differential Equations: An Introduction. New York: Dover, 1989.
Hahn, W. Theory and Application of Liapunov's Direct Method. Englewood Cliffs, NJ: Prentice-Hall, 1963.
Jordan, D. W. and Smith, P. Nonlinear Ordinary Differential Equations. Oxford, England: Clarendon Press, p. 283, 1977.
Kalman, R. E. and Bertram, J. E. "Control System Analysis and Design Via the 'Second Method' of Liapunov, I. Continuous-Time Systems." J. Basic Energ. Trans. ASME 82, 371-393, 1960.
Oguztöreli, M. N.; Lakshmikantham, V.; and Leela, S. "An Algorithm for the Construction of Liapunov Functions." Nonlinear Anal.5, 1195-1212, 1981.
Zwillinger, D. "Liapunov Functions." §120 in Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, pp. 429-432, 1997.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|