Simple Harmonic Motion
المؤلف:
GEORGE A. HOADLEY
المصدر:
ESSENTIALS OF PHYSICS
الجزء والصفحة:
p-178
2025-11-12
16
If a heavy ball, suspended like a pendulum, is given a circular motion in a horizontal plane, the cord by which it is suspended will describe the surface of a cone, and the arrangement is called a conical pendulum. To an eye at E, in the same horizontal plane as that in which the ball is moving, the ball seems to be moving in a horizontal straight line, projected on the wall at АВ.
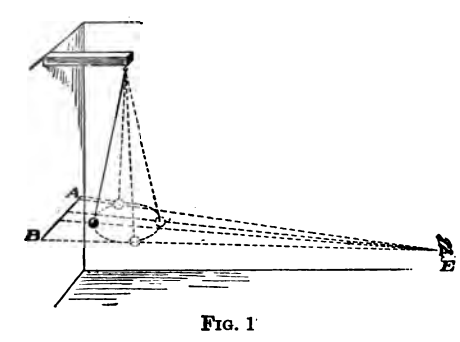
Though the ball is moving with uniform velocity around its circular path, the projected motion is a to-and-fro motion, like that of an ordinary pendulum. The velocity of this projected motion is greatest at the middle of the path AB and decreases to zero at A or B.
If the path of the ball is represented by the circle in Fig. 2, the corresponding position on the line AB, at any time, can be found as follows, if we assume that E is at a distance so great that the lines EA and EB are practically parallel: divide the circle into any convenient number of parts, 16, for example. From the dividing points 1, 2, 3, etc., drop perpendiculars to the line AB, meeting it at the corresponding points 1', 2', 3', etc. Anybody moving to and fro along the line AB in such a way that its position at any time corresponds to the projection on AB of a body moving with uniform velocity around the circle of reference, is said to have a simple harmonic motion. It is evident that the distances 1'-2', 2'-3', etc., are passed over in equal times.
الاكثر قراءة في الميكانيك
اخر الاخبار
اخبار العتبة العباسية المقدسة
